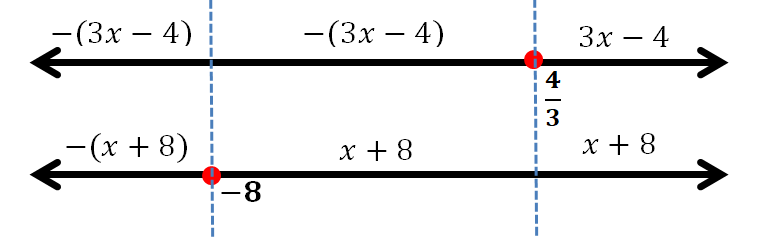Selesaikan pertidaksamaan dari ∣ x + 8∣ > ∣3 x − 4∣ .

Pembahasan

Diberikan pertidaksamaan ∣ x + 8∣ > ∣3 x − 4∣ . Untuk ∣ x + 8∣ , didapat nilai sebagai berikut. ∣ x + 8 ∣ = { ( x + 8 ) , ( x + 8 ) ≥ 0 atau x ≥ − 8 − ( x + 8 ) , ( x + 8 ) < 0 atau x < − 8 ​ Terdapat perubahan nilai saat x < − 8 dan x ≥ − 8 . Sehingga terdapat dua daerah himpunan penyelesaian yang mungkin. Kemudian untuk ∣ 3 x − 4 ∣ , didapat nilai sebagai berikut. ∣ 3 x − 4 ∣ = { ( 3 x − 4 ) , ( 3 x − 4 ) ≥ 0 atau x ≥ 3 4 ​ − ( 3 x − 4 ) , ( 3 x − 4 ) < 0 atau x < 3 4 ​ ​ Terdapat perubahan nilai saat x < 3 4 ​ dan x ≥ 3 4 ​ . Sehingga terdapat dua daerah himpunan penyelesaian yang mungkin. Gabungandaerah dari nilai x di atas menghasilkan 3 daerah sebagai berikut. 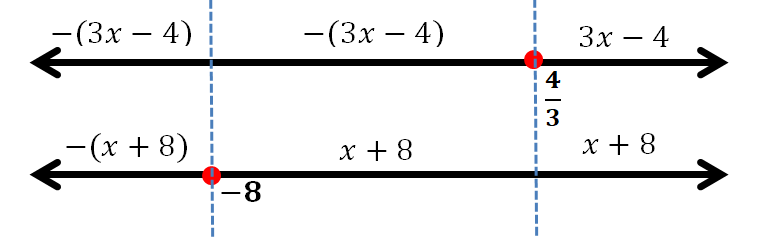Daerah I. Untuk interval x < − 8 , didapat hasil perhitungan sebagai berikut. − ( x + 8 ) > − ( 3 x − 4 ) − x − 8 > − 3 x + 4 − x + 3 x > 4 + 8 2 x > 12 x > 6 Karena irisan dari x < − 8 dan x > 6 tidak ada, maka tidak terdapat penyelesaian dari kasus ini. Daerah II. Untuk inteval − 8 ≤ x < 3 4 ​ , didapathasil perhitungan sebagai berikut. ( x + 8 ) > − ( 3 x − 4 ) x + 8 > − 3 x + 4 x + 3 x > 4 − 8 4 x > − 4 x > 4 − 4 ​ x > − 1 Karena irisan dari − 8 ≤ x < 3 4 ​ dan x > − 1 adalah − 1 < x < 3 4 ​ , maka penyelesaiannya adalah − 1 < x < 3 4 ​ Daerah III. Untuk interval x ≥ 3 4 ​ , didapathasil perhitungan sebagai berikut. ( x + 8 ) > ( 3 x − 4 ) x + 8 > 3 x − 4 x − 3 x > − 4 − 8 − 2 x > − 12 x < − 2 − 12 ​ x < 6 Karena irisan dari x ≥ 3 4 ​ dan x < 6 adalah 3 4 ​ ≤ x < 6 , maka penyelesaiannya adalah 3 4 ​ ≤ x < 6 . Jika kita gabungkan interval − 1 < x < 3 4 ​ dan 3 4 ​ ≤x<6 , diperoleh daerah himpunan penyelesaiannya adalah − 1 < x < 6 Dengan demikian, penyelesaian dari pertidaksamaan ∣ x + 8∣ > ∣3 x − 4∣ adalah − 1 < x < 6 .