Pertanyaan

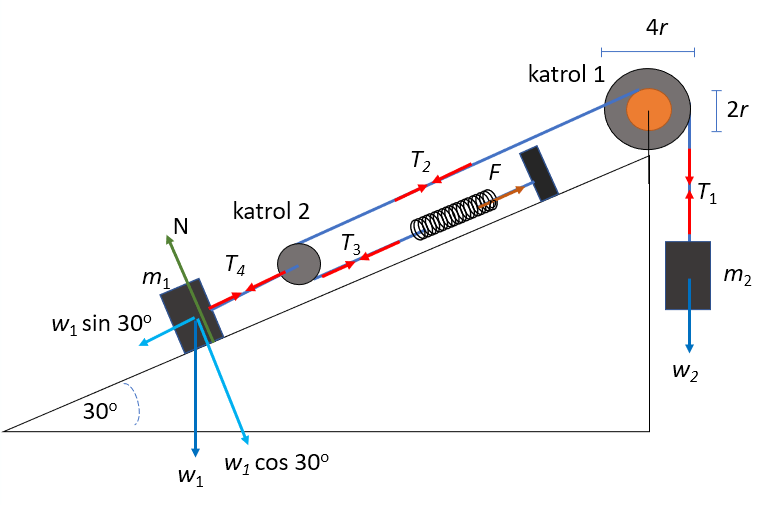
Sebuah sistem mekanik diperlihatkan pada gambar. Sudut kemiringan bidang θ = 30° dan bidang miring licin. Sistem berada dalam keadaan setimbang serta massa katrol dan massa pegas diabaikan. Jika setiap massa dijadikan dua kali semula, salah satu cara yang dapat dilakukan agar sistem tetap setimbang adalah ….

Sebuah sistem mekanik diperlihatkan pada gambar.

Sudut kemiringan bidang θ = 30° dan bidang miring licin. Sistem berada dalam keadaan setimbang serta massa katrol dan massa pegas diabaikan. Jika setiap massa dijadikan dua kali semula, salah satu cara yang dapat dilakukan agar sistem tetap setimbang adalah ….

konstanta pegas tetap dan pertambahan panjang pegas menjadi 2 kali semula
konstanta pegas menjadi 0,5 kali semula dan pertambahan panjang pegas menjadi 2 kali semula
konstanta pegas tetap dan pertambahan panjang pegas menjadi setengah kali semula
konstanta pegas menjadi 2 kali semula dan pertambahan panjang pegas tetap
konstanta pegas tetap dan pertambahan panjang pegas menjadi 4 kali semula

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

Y. Maghfirah

Master Teacher

Jawaban terverifikasi

Jawaban

jawaban yang tepat adalah D.

Pembahasan

Perhatikan diagram bebas gaya pada sistem berikut. Tinjau massa m 2 , berlaku kesetimbangan translasi Σ F = 0 T 1 − W 2 = 0 T 1 = W 2 T 1 = m 2 . g ...... ( 1 ) Tinjau katrol 1, berlaku kesetimbangan rotasi Σ τ = 0 T 1 .2 r − T 2 . r = 0 T 1 .2 r = T 2 . r T 1 = 2 1 T 2 ...... ( 2 ) Substitusi pers. (1) ke pers. (2) m 2 . g = 2 1 T 2 T 2 = 2 m 2 . g ...... ( 3 ) Tinjau katrol 2, berlaku kesetimbangan rotasi dan translasi kesetimbangan rotasi: Σ τ = 0 T 3 . R − T 2 . R = 0 T 3 . R = T 2 . R T 3 = T 2 ...... ( 4 ) esetimbangan translasi: Σ F = 0 T 2 + T 3 − T 4 = 0 T 2 + T 3 = T 4 dari pers. (3) diketahui bahwa T 2 = T 3, maka T 2 + T 3 = T 4 T 3 + T 3 = T 4 2 T 3 = T 4 T 3 = 2 1 T 4 ...... ( 5 ) Tinjau benda m 1 , berlaku kesetimbangan translasi Σ F = 0 T 4 − w 1 sin 3 0 ∘ = 0 T 4 = w 1 sin 3 0 ∘ T 4 = m 1 . g . 2 1 T 4 = 2 1 m 1 . g ...... ( 6 ) Tinjau pegas, berlaku persamaan kesetimbangan translasi Σ F = 0 T 4 − F = 0 T 4 = F T 4 = k . x ...... ( 7 ) Berdasarkan pers. (4) dan pers. (5) diperoleh hubungan T 2 = T 3 = 2 1 T 4 2 m 2 . g = 4 1 m 1 . g = k . x Dari persamaan tersebut kita bisa menyimpulkan bahwa m 2 , m 1 , dan k berbanding lurus. Apabilam 1 dan m 2 diubah menjadi 2 kali lipat dansistem tetap setimbang ( x bernilai tetap) , maka konstanta pegas k dijadikan 2 kali lipat. Jadi, jawaban yang tepat adalah D.

Perhatikan diagram bebas gaya pada sistem berikut.

Tinjau massa m₂, berlaku kesetimbangan translasi

$Σ F = 0 T_{1} - W_{2} = 0 T_{1} = W_{2} T_{1} = m_{2} . g ...... (1)$

Tinjau katrol 1, berlaku kesetimbangan rotasi

$Σ τ = 0 T_{1} .2 r - T_{2} . r = 0 T_{1} .2 r = T_{2} . r T_{1} = \frac{1}{2} T_{2} ...... (2)$

Substitusi pers. (1) ke pers. (2)

$m_{2} . g = \frac{1}{2} T_{2} T_{2} = 2 m_{2} . g ...... (3)$

Tinjau katrol 2, berlaku kesetimbangan rotasi dan translasi

kesetimbangan rotasi:

$Σ τ = 0 T_{3} . R - T_{2} . R = 0 T_{3} . R = T_{2} . R T_{3} = T_{2} ...... (4)$

esetimbangan translasi:

$Σ F = 0 T_{2} + T_{3} - T_{4} = 0 T_{2} + T_{3} = T_{4}$

dari pers. (3) diketahui bahwa T₂= T_{3, maka}

$T_{2} + T_{3} = T_{4} T_{3} + T_{3} = T_{4} 2 T_{3} = T_{4} T_{3} = \frac{1}{2} T_{4} ...... (5)$

Tinjau benda m₁, berlakukesetimbangan translasi

$Σ F = 0 T_{4} - w_{1} sin 3 0^{\circ} = 0 T_{4} = w_{1} sin 3 0^{\circ} T_{4} = m_{1} . g . \frac{1}{2} T_{4} = \frac{1}{2} m_{1} . g ...... (6)$

Tinjau pegas, berlaku persamaan kesetimbangan translasi

$Σ F = 0 T 4 - F = 0 T 4 = F T 4 = k . x ...... (7)$

Berdasarkan pers. (4) dan pers. (5) diperoleh hubungan

$T_{2} = T_{3} = \frac{1}{2} T_{4} 2 m_{2} . g = \frac{1}{4} m_{1} . g = k . x$

Dari persamaan tersebut kita bisa menyimpulkan bahwa m₂, m₁, dan k berbanding lurus. Apabila m₁ dan m₂ diubah menjadi 2 kali lipat dan sistem tetap setimbang (x bernilai tetap) , maka konstanta pegas k dijadikan 2 kali lipat.

Jadi, jawaban yang tepat adalah D.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

0.0 (0 rating)

Pertanyaan serupa

Sebuah benda pada permukaan dalam sebuah mangkok licin berbentuk setengah bola berotasi dengan kecepatan sudut konstan ωterhadap sumbu vertikal (lihat gambar). Diketahui jari-jari mangkok 60 cm ...

0.0

Jawaban terverifikasi

Sebuah pegas dengan konstanta 1000 N/m dipasang horizontal di bidang datar licin. Sebuah balok dengan massa 225 gram didorong menekan pegas sejauh x, lalu dilepas. Kecepatan balok setelah lepas dari p...

0.0

Jawaban terverifikasi

Sebuah benda bergerak pada bidang xy dengan kecepatan v x ( t ) = 6 t − 2 dan v y ( t ) = 2 t + 6 . Diketahui pada saat t = 0, benda berada di x 0 = 1 m dan y 0 = 2 m.Dengan demikianpada saat t = ...

0.0

Jawaban terverifikasi

0.0

Jawaban terverifikasi

0.0

Jawaban terverifikasi