Perhatikan grafikberikut ini! Rumus fungsi eksponen yang sesuai untuk gambar grafik di atas adalah ....

Pembahasan

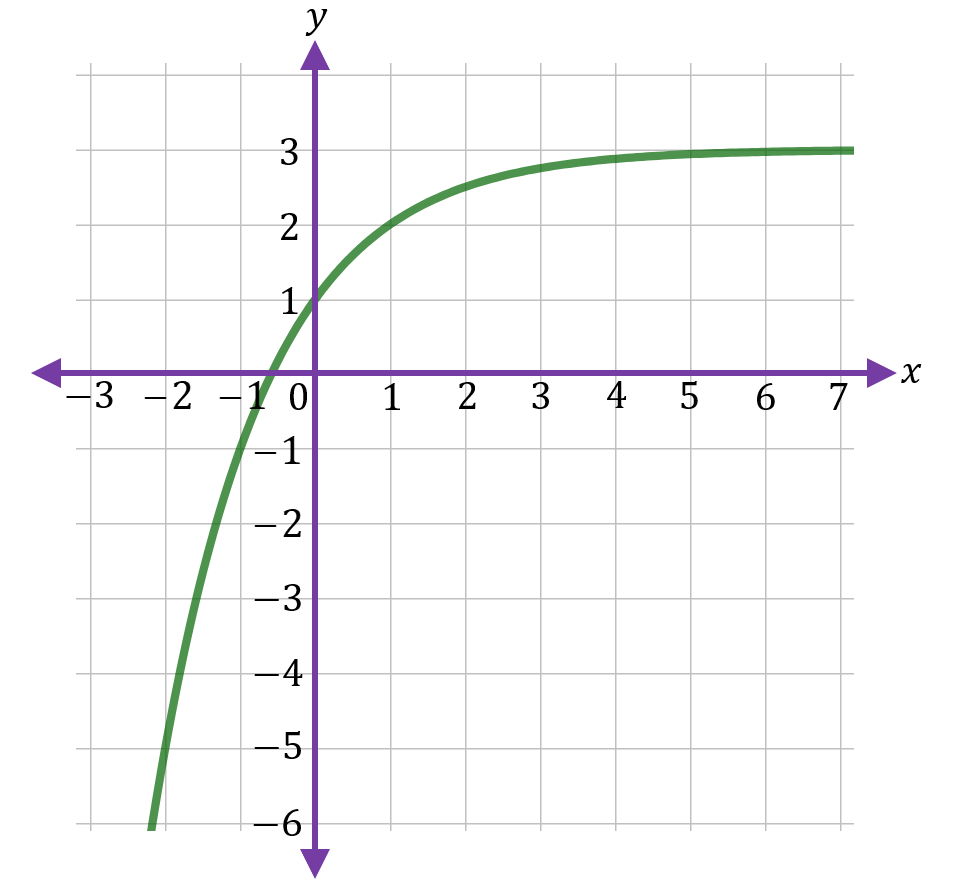
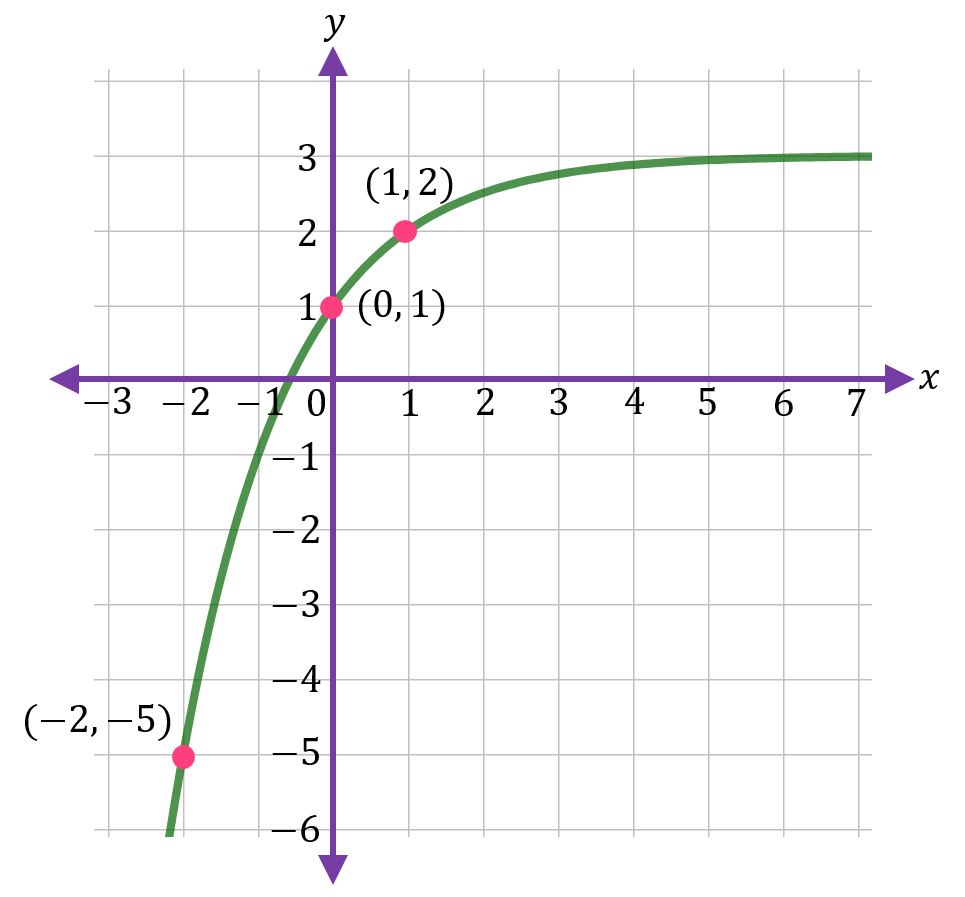
Dari gambar yang diberikan, perhatikan bahwa salah satu ujung grafik mendekati y = 3 sehingga bentuk umum dari fungsi eksponen untuk grafik tersebut adalah f ( x ) = a ⋅ b x + c . Untuk menentukan rumus fungsi ekponen dari grafik tersebut, terdapat beberapa langkah yang diperlukan seperti di bawah ini. Langkah Pertama: Tentukan nilai , b , dan . Perhatikan gambar berikut ini! Titik ( 1 , 2 ) , ( 0 , 1 ) , dan ( − 2 , − 5 ) akan digunakan untuk mencari nilai , b , dan . Selanjutnya, perhatikan perhitungan berikut! ( 1 , 2 ) ( 0 , 1 ) ( − 2 , − 5 ) ​ ⇒ ⇒ ⇒ ​ 2 = a ⋅ b 1 + c 1 = a ⋅ b 0 + c − 5 = a ⋅ b − 2 + c ​ ⇒ ⇒ ⇒ ​ 2 = ab + c 1 = a + c − 5 = a b − 2 + c ​ ... ( i ) ... ( ii ) ... ( iii ) ​ Kemudian, kurangkan persamaan (i) dengan persamaan (ii) dan persamaan (iii) dengan persamaan (ii) untuk mengeliminasi seperti berikut ini. ab + c = 2 a + c = 1 ​ ab − a = 1 a ( b − 1 ) = 1 ​ − ... ( iv ) ​ ​ dan ​ ​ a + c = 1 b 2 a ​ + c = − 5 ​ a − b 2 a ​ = 6 b 2 a b 2 − a ​ = 6 b 2 a ( b 2 − 1 ) ​ = 6 b 2 a ( b − 1 ) ( 1 + b ) ​ = 6 ​ − ... ( v ) ​ ​ Substitusi persamaan (iv) ke persamaan (v) sehingga diperoleh perhitungan berikut. b 2 a ( b − 1 ) ( b + 1 ) ​ a ( b − 1 ) ( b + 1 ) 1 ⋅ ( b + 1 ) − 6 b 2 + b + 1 6 b 2 − b − 1 ( 2 b − 1 ) ( 3 b + 1 ) b = 2 1 ​ atau b ​ = = = = = = = ​ 6 6 b 2 6 b 2 0 0 0 − 3 1 ​ ​ Ingat kembali bahwa untuk b < 0 tidak memenuhi syarat fungsi eksponen f ( x ) = a ⋅ b x + c sehingga diperoleh nilai b = 2 1 ​ . Selanjutnya, substitusi nilai b = 2 1 ​ ke persamaan (i) dan kurangkan persamaan (i) dengan persamaan (ii) sehingga diperoleh perhitungan berikut. Didapat nilai c = 3 . Substitusi nilai c = 3 ke persamaan (ii) sehingga diperoleh nilai sebagai berikut. a + c a + 3 a ​ = = = ​ 1 1 − 2 ​ Didapat nilai a = − 2 . Langkah Kedua: Tentukan rumus fungsi eksponen. Karena nilai a = − 2 , b = 2 1 ​ , dan c = 3 , makadiperoleh rumus fungsi eksponen sebagai berikut. f ( x ) ​ = = = = = ​ a ⋅ b x + c − 2 ⋅ ( 2 1 ​ ) x + 3 − 1 ⋅ 2 ⋅ ( 2 − 1 ) x + 3 − 1 ⋅ 2 ⋅ 2 − x + 3 − 2 1 − x + 3 ​ Dengan demikian, rumusfungsi eksponen yang sesuai adalah f ( x ) = − 2 1 − x + 3 . Jadi, jawaban yang tepat adalah C.