Pertanyaan

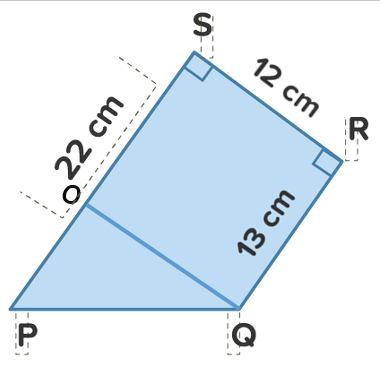
Perhatikan gambar berikut! Diketahui Trapesium KLMN dan Trapesium PQRS adalah kongruen. Maka panjang PQ adalah ...

Perhatikan gambar berikut!

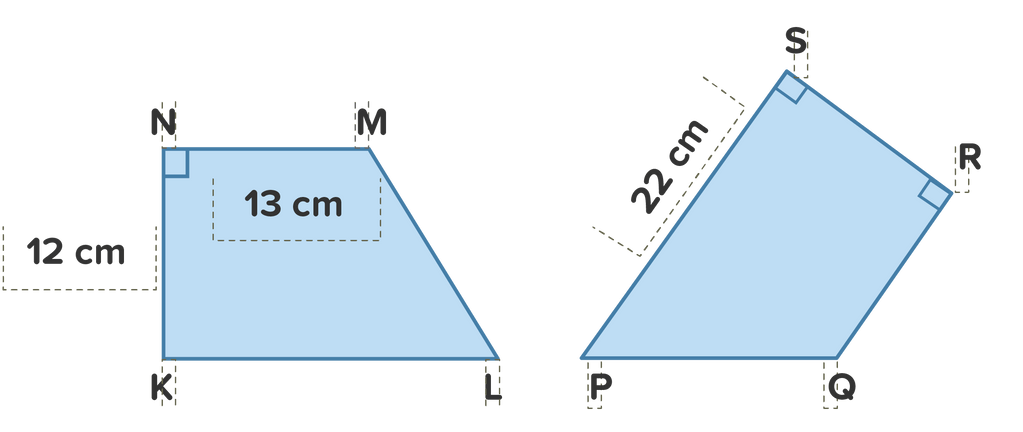
Diketahui Trapesium KLMN dan Trapesium PQRS adalah kongruen. Maka panjang PQ adalah ...

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

S. Ayu

Master Teacher

Mahasiswa/Alumni Universitas Muhammadiyah Prof. DR. Hamka

Jawaban terverifikasi

Pembahasan

Dua buah bangun datar dapat dikatakan kongruen jika memenuhi dua syarat, yaitu: Sudut-sudut yang bersesuaian sama besar. Sisi-sisi yang bersesuaian sama panjang. Diketahui: Trapesium KLMN dan Trapesium PQRS adalah kongruen. Sisi-sisi yang bersesuaian pada trapesium KLMN dan trapesium PQRS sama panjang, yaitu: Pada trapesiumPQRS diperoleh bahwa: Perhatikan yang berbentuk siku-siku. Tentukan terlebih dahulu panjang sisi OP, yaitu: Gunakan Teorema Pythagoras untuk mengetahui panjang sisi PQ seperti berikut: Maka, panjang PQ adalah .

Dua buah bangun datar dapat dikatakan kongruen jika memenuhi dua syarat, yaitu:

Sudut-sudut yang bersesuaian sama besar.
Sisi-sisi yang bersesuaian sama panjang.

Diketahui:

Trapesium KLMN dan Trapesium PQRS adalah kongruen.

Sisi-sisi yang bersesuaian pada trapesium KLMN dan trapesium PQRS sama panjang, yaitu:

Pada trapesiumPQRS diperoleh bahwa:

Perhatikan yang berbentuk siku-siku.

Tentukan terlebih dahulu panjang sisi OP, yaitu:

begin mathsize 14px style table attributes columnalign right center left columnspacing 0px end attributes row OP equals cell PS minus QR end cell row OP equals cell 22 space cm minus 13 space cm end cell row OP equals cell 9 space cm end cell end table end style

Gunakan Teorema Pythagoras untuk mengetahui panjang sisi PQ seperti berikut:

Maka, panjang PQ adalah .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

5.0 (1 rating)

Pertanyaan serupa

Diketahui trapesium KLMN dan trapesium PQRS adalah kongruen. Maka panjang PQ adalah ....

4.6

Jawaban terverifikasi

Diketahui trapesium ABCD dan trapesium FEHG adalah kongruen. Jika panjang sisi A D = 12 cm , C D = 13 cm , dan EF = 22 cm , maka tentukan panjang EH .

4.8

Jawaban terverifikasi

Pada gambar berikut, jika PQRS kongruen dengan UVRT dan panjang RT = 4 3 SP , maka panjang PQ adalah ....

4.6

Jawaban terverifikasi

Perhatikan gambar di bawah ini! Pasangan segitiga yang kongruen adalah ...

3.6

Jawaban terverifikasi

Dari gambar dua bangun datar berikut yang kongruen, sisi-sisi yang bersesuaiannya adalah ....

5.0

Jawaban terverifikasi