Pertanyaan

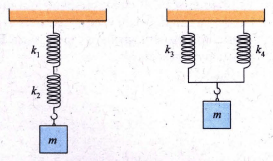
Pegas disusun secara seri dan paralel seperti gambar berikut. Ujung pegas digantungi beban yang sama besar. Jika konstanta pegas k 1 = k 2 = k 3 = k 4 = k maka perbandingan periode susunan seri dan paralel adalah....

Pegas disusun secara seri dan paralel seperti gambar berikut.

Ujung pegas digantungi beban yang sama besar. Jika konstanta pegas k₁ = k₂ = k₃ = k₄ = k maka perbandingan periode susunan seri dan paralel adalah....

5 : 4
2 : 1
3 : 2
1 : 2
2 : 3

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

N. Puspita

Master Teacher

Jawaban terverifikasi

Jawaban

jawaban yang tepat adalah B

Pembahasan

Periode Pegas dituliskan dalam persamaan : Konstanta total pegas untuk setiap susunan sebesar : Seri Paralel Kemudian perbandingan periode dapat dihitung : Maka,perbandingan periode susunan seri dan paralel adalah 2 : 1. Jadi, jawaban yang tepat adalah B

Periode Pegas dituliskan dalam persamaan :

begin mathsize 14px style bold italic T bold space bold equals bold space bold 2 bold pi bold space square root of bold italic m over bold italic k end root end style

Konstanta total pegas untuk setiap susunan sebesar :

Seri

Paralel

Kemudian perbandingan periode dapat dihitung :

$begin mathsize 14px style table attributes columnalign right center left columnspacing 0px end attributes row cell T subscript s over T subscript p space end cell equals cell space fraction numerator 2 straight pi space square root of begin display style m over k subscript s end style end root over denominator 2 straight pi space square root of begin display style m over k subscript p end style end root end fraction end cell row cell T subscript s over T subscript p space end cell equals cell space fraction numerator square root of begin display style m over k subscript s end style end root over denominator square root of begin display style m over k subscript p end style end root end fraction space space space bold asterisk times bold kuadratkan bold space bold kedua bold space bold sisi end cell row cell open parentheses T subscript s over T subscript p close parentheses squared space end cell equals cell space fraction numerator begin display style m over k subscript s end style over denominator begin display style m over k subscript p end style end fraction end cell row cell open parentheses T subscript s over T subscript p close parentheses squared space end cell equals cell space fraction numerator begin display style fraction numerator m over denominator begin display style bevelled k over 2 end style end fraction end style over denominator begin display style fraction numerator m over denominator 2 k end fraction end style end fraction end cell row cell open parentheses T subscript s over T subscript p close parentheses squared space end cell equals cell space fraction numerator 2 m over denominator k end fraction space cross times space fraction numerator 2 k over denominator m end fraction end cell row cell open parentheses T subscript s over T subscript p close parentheses squared space end cell equals cell space 4 over 1 end cell row cell T subscript s over T subscript p space end cell equals cell space square root of 4 over 1 end root space equals space bold 2 over bold 1 end cell end table end style$

Maka, perbandingan periode susunan seri dan paralel adalah 2 : 1.

Jadi, jawaban yang tepat adalah B

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.7 (27 rating)

Hanna Safira

Ini yang aku cari!

Najwa Nia Aulia

Makasih ❤️

Vifin Oktaviani

Pembahasan lengkap banget

salsaabill

Ini yang aku cari!

Natasya Fanesia

Pembahasan lengkap banget Makasih ❤️

Pertanyaan serupa

Dua pegas identik mula-mula disusun seri lalu kemudian disusun paralel.Kedua susunan pegas itu digantung oleh beban yang berbeda. Untuk menghasilkan pertambahan panjang sistem pegas paralel dan sistem...

4.8

Jawaban terverifikasi

3 pegas identik disusun seperti gambar di bawah ini Perbandingan perubahan panjang pegas susunan A dan B adalah... (Beban kedua sistem sama besar)

4.0

Jawaban terverifikasi

3 pegas identik disusun seperti gambar di bawah ini Perbandingan perubahan panjang pegas susunan A dan B adalah... (Beban kedua sistem sama besar)

4.0

Jawaban terverifikasi

4.8

Jawaban terverifikasi

Sebuah pegas dengan nilai tetapan pegas sebesar 2.000 N/m dipotong menjadi 4 bagian yang sama besar (identik). Besar tetapan pegas sekarang adalah …

0.0