Pertanyaan

Pada segitiga ABC , BM tegak lurus dengan AC , CN tegak lurus dengan AB . Panjang BM = CN . Tunjukkan bahwa △ BCM = △ CBN !

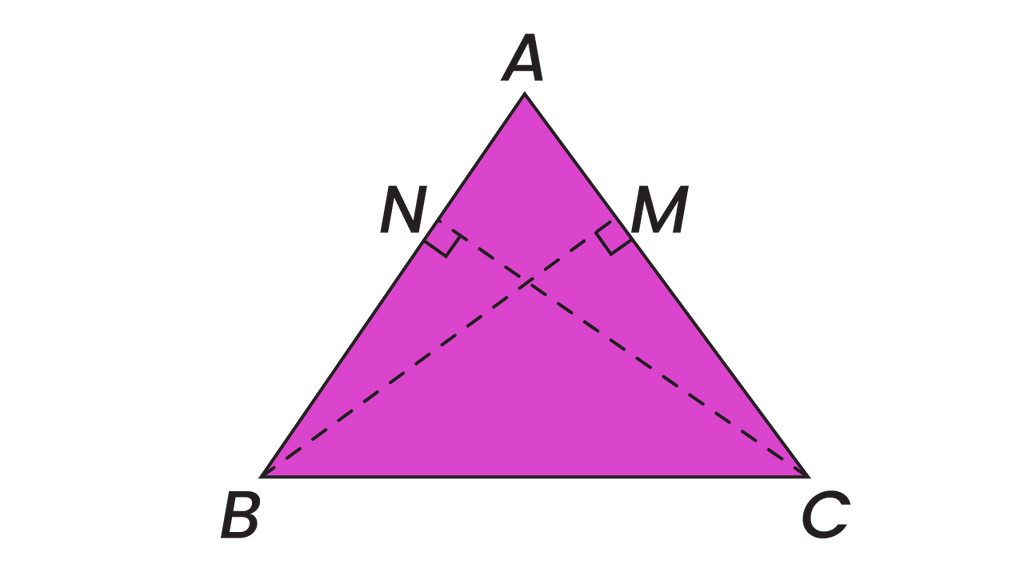
Pada segitiga $ABC, BM$ tegak lurus dengan $AC, CN$ tegak lurus dengan $AB .$ Panjang $BM = CN .$ Tunjukkan bahwa $△ BCM = △ CBN!$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

A. Salim

Master Teacher

Mahasiswa/Alumni Universitas Pelita Harapan

Jawaban terverifikasi

Jawaban

pada soal tersebut adalah benar terbukti.

pada soal tersebut adalah benar terbukti.

Pembahasan

Untuk membuktikan bahwa dua segitiga kongruen (sama dan sebangun), kita cukup menunjukkan kedua segitiga memenuhi salah satu dari syaratberikut: sisi-sisi-sisi sudut-sisi-sudut sisi-sudut-sisi Perhatikan segitiga dan segitiga Diketahui bahwa salah satu sisisegitiga dan segitiga saling berhimpitan yaitu sisi Kemudian, diketahui bahwa Karenasegitiga dan segitiga merupakan segitiga siku-siku, maka berlaku aturan teorema pythagoras sebagai berikut: Untuk segitiga berlaku rumus berikut: Untuk segitiga dan diketahui berlaku: Sehingga, panjang Berdasarkan uraian di atas, syaratsisi-sisi-sisi sudah terpenuhi. Sehingga,segitiga dan segitiga adalah kongruen. Dengan demikian, pada soal tersebut adalah benar terbukti.

Untuk membuktikan bahwa dua segitiga kongruen (sama dan sebangun), kita cukup menunjukkan kedua segitiga memenuhi salah satu dari syarat berikut:

sisi-sisi-sisi
sudut-sisi-sudut
sisi-sudut-sisi

Perhatikan segitiga CBN dan segitiga BCM.

Diketahui bahwa salah satu sisi segitiga CBN dan segitiga BCM saling berhimpitan yaitu sisi BC space open parentheses sisi close parentheses. Kemudian, diketahui bahwa BM equals CN space open parentheses sisi close parentheses. Karena segitiga CBN dan segitiga BCM merupakan segitiga siku-siku, maka berlaku aturan teorema pythagoras sebagai berikut:

Untuk segitiga CBN berlaku rumus berikut:

table attributes columnalign right center left columnspacing 0px end attributes row cell BC squared end cell equals cell BN squared plus CN squared end cell row blank left right double arrow cell BN squared equals BC squared minus CN squared end cell row blank blank blank end table

Untuk segitiga BCM dan diketahui BM equals CN berlaku:

Sehingga, panjang CM equals BN space open parentheses sisi close parentheses.

Berdasarkan uraian di atas, syarat sisi-sisi-sisi sudah terpenuhi. Sehingga, segitiga CBN dan segitiga BCM adalah kongruen.

Dengan demikian, increment BCM equals increment CBN pada soal tersebut adalah benar terbukti.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.8 (21 rating)

Caca Rohma

Mudah dimengerti Makasih ❤️

Anon

Ini yang aku cari! Pembahasan lengkap banget Mudah dimengerti Makasih ❤️

Ananda Syiva Rosita

Makasih ❤️ Mudah dimengerti Ini yang aku cari!

Selly Herprianti

Pembahasan lengkap banget Ini yang aku cari! Mudah dimengerti Bantu banget Makasih ❤️

Wijaya Adi Shankara

Pembahasan lengkap banget

Pertanyaan serupa

Perhatikan gambar layang-layang ABCD berikut. Pada gambar di atas, dapat disimpulkan bahwa segitiga ABC dan segitiga ACD ....

0.0

Jawaban terverifikasi

Pada gambar di atas, PQ=SR dan PS=RQ . b. Sebutkan pasangan sudut yang sama

4.1

Jawaban terverifikasi

Bangun WXYZ adalah segiempat dengan sisi-sisi WXZY yang berhadapan panjangnya sama. XZ adalah salah satu diagonalnya. a. Tunjukkan bahwa △ WXZ ≅ △ ZYX

4.6

Jawaban terverifikasi

Diketahui panjang BC = CD . △ CDA ≅ △ CBE menurut aksioma ....

4.8

Jawaban terverifikasi

Perhatikan gambar berikut! Pada gambar berikut Segitiga ABC kongruen dengan segitiga ADC karena memenuhi syarat...

5.0

Jawaban terverifikasi