Untuk menjawab soal diatas, ingat konsep pertidaksamaan logaritma berikut:
- Jika basis logaritma a>1, maka solusi dari alog f(x)≤alog g(x) menjadi f(x)≤g(x), dengan syarat f(x)>0 dan g(x)>0.
Dari soal diketahui pertidaksamaan xlog (x2+4x+4)≤xlog (5x+10), jika basis logaritmanya a>1 maka:
xlog (x2+4x+4)x2+4x+4x2+4x−5x+4−10x2−x−6(x−3)(x+2)≤≤≤≤≤xlog (5x+10)5x+10000
Misalkan (x−3)(x+2)=0, maka:
(x−3)(x+2)x1x2===03 −2
Kemudian buatlah garis bilangan dengan nilai x1 dan x2 dengan keduanya memiliki bulatan yang penuh agar dapat memenuhi persamaan (x−3)(x+2)≤0 seperti berikut:
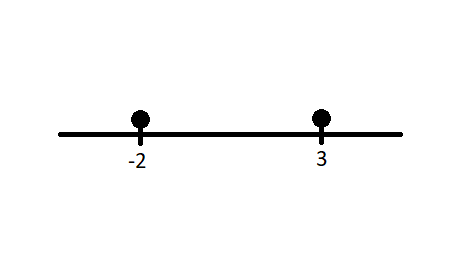
Dari garis bilangan didapatkan tiga ruas yakni x≤−2, −2≤x≤3, dan x≥3. Kemudian dilakukan uji titik untuk menentukan daerah yang memenuhi pertidaksamaan (x−3)(x+2)≤0:
- Saat x≤−2, uji titik x=−3:
(x−3)(x+2)⇒((−3)−3)((−3)+2)=(−6)(−1)=6>0
Ruas x≤−2 tidak memenuhi pertidaksamaan.
- Saat −2≤x≤3, uji titik x=0:
(x−3)(x+2)⇒((0)−3)((0)+2)=(−3)(2)=−6<0
Ruas −2≤x≤3 memenuhi pertidaksamaan.
(x−3)(x+2)⇒((4)−3)((4)+2)=(1)(6)=6>0
Ruas x≥3 tidak memenuhi pertidaksamaan.
Berdasarkan uji titik, garis bilangan yang sesuai untuk pertidaksamaan (x−3)(x+2)≤0 adalah:
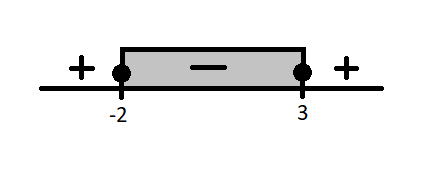
Setelah itu, dilihat syarat numerus logaritmanya:
x2+4x+4(x+2)2x>>>00 −2
5x+105xx>>>0−10 −2
Dengan ini, garis bilangan syarat numerus dapat digambarkan seperti berikut:

Syarat basis logaritma adalah a>1. Dari persamaan xlog (x2+4x+4)≤xlog (5x+10) maka basis haruslah x>1, dimana garis bilangan dapat digambarkan seperti berikut:

Setelah solusi, syarat numerus, serta syarat basis sudah memenuhi pertidaksamaan, maka himpunan penyelesaian pertidaksamaan dapat digambarkan seperti berikut:
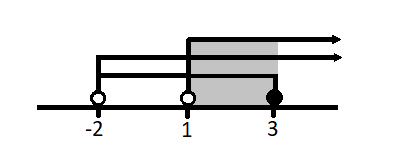
Dari garis bilangan, terlihat bahwa nilai x yang memenuhi pertidaksamaan xlog (x2+4x+4)≤xlog (5x+10) adalah 1<x≤3.
Oleh karena itu, tidak ada jawaban yang benar.




















