Gunakan konsep rumus cosinus jumlah dua sudut, perbandingan sisi trigonometri, relasi sudut  .
.

Ingat kembali nilai trigonometri sudut istimewa  dan
dan  .
.

Diketahui segitiga  adalah segitiga sama kaki dengan
adalah segitiga sama kaki dengan  dan
dan  .
.
*Terlebih dahulu tentukan sisi depan dan sisi miring dari nilai sinus yang diketahui.

Diperoleh sisi depan dan sisi miring sudut  adalah
adalah  dan
dan  .
.
Agar lebih mudah ilustrasikan terlebih dahulu informasi yang diketahui menjadi sebagai berikut.
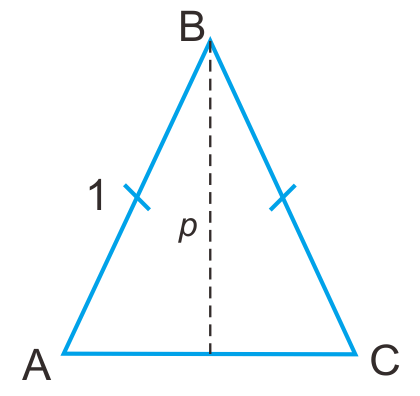
a. Menentukan batas nilai 
Sudut  harus berada antara
harus berada antara  dan
dan  untuk menjadi segitiga sama kaki, sehingga diperoleh sebagai berikut.
untuk menjadi segitiga sama kaki, sehingga diperoleh sebagai berikut.

Jadi, diperoleh bahwa batas nilai  adalah
adalah  .
.
b. Menentukan  .
.
Karena segitiga tersebut sama kaki, maka besar  , sehingga diperoleh:
, sehingga diperoleh:

Jadi, diperoleh nilai  .
.
c. Menentukan 
Terlebih dahulu tentukan sisi samping sudut  dengan menggunakan teorema Pythagoras, diperoleh sebagai berikut.
dengan menggunakan teorema Pythagoras, diperoleh sebagai berikut.

Diperoleh sisi samping sudut  adalah
adalah  , sehingga nilai
, sehingga nilai  dapat dihitung sebagai berikut.
dapat dihitung sebagai berikut.

Diperoleh nilai 
d. Menentukan 
Karena segitiga tersebut sama kaki, maka besar  , sehingga diperoleh:
, sehingga diperoleh:

Jadi, diperoleh nilai  .
.
e. Menentukan 
Ingat bahwa jumlah sudut dalam segitiga adalah  , sehingga diperoleh sebagai berikut.
, sehingga diperoleh sebagai berikut.

Untuk menentukan nilai  dapat diperoleh dengan cara.
dapat diperoleh dengan cara.

Sehingga untuk menentukan nilai  dapat diperoleh dengan menghitung nilai
dapat diperoleh dengan menghitung nilai  .
.

Jadi, diperoleh nilai  .
.
f. Menentukan 
Untuk menentukan nilai  dapat diperoleh dengan cara.
dapat diperoleh dengan cara.

Sehingga untuk menentukan nilai  dapat diperoleh dengan menghitung nilai
dapat diperoleh dengan menghitung nilai  .
.

Jadi, diperoleh nilai  .
.
















