Lanjutkan pola bilangan berikut. Apakah tiga bilangan yang diperoleh membentuk tripel Pythagoras? Apa Kesimpulanmu?

Pembahasan

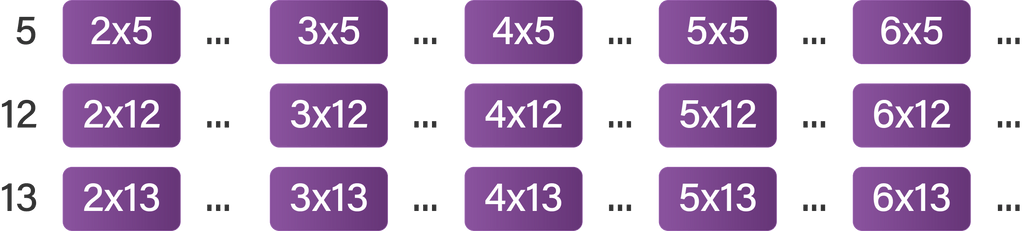
Jawaban yang benar untuk pertanyaan tersebut adalah tigabilangan yang diperoleh membentuk tripel Pythagoras dan dapat disimpulkan bahwakelipatan dari tripel Pythagoras juga merupakan tripel Pythagoras. Tripel Pythagoras merupakan kelompok tiga bilangan asli yang memenuhi ketentuan, yaitu kuadrat bilangan terbesar sama dengan jumlah kuadrat dua bilangan lainnya. c 2 = a 2 + b 2 dengan bilangan terbesar. Pola bilangan di atas dapat dilengkapi sebagai berikut. 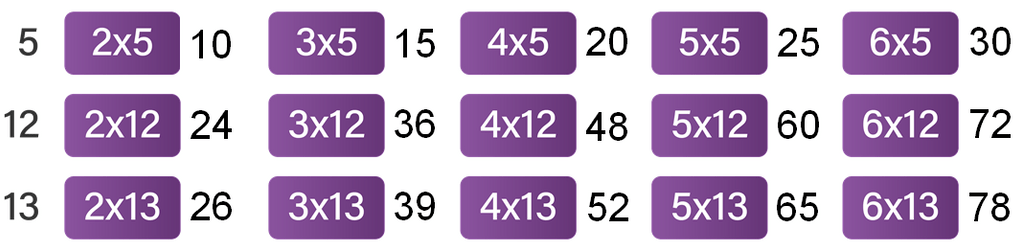Kelompok bilangan yang terbentuk, yaitu ( 10 , 24 , 26 ) , ( 15 , 36 , 39 ) , ( 20 , 48 , 52 ) , ( 25 , 60 , 65 ) , dan ( 30 , 72 , 78 ) . Berdasarkan definisi tripel Pythagoras dapat ditentukan hubungan berikut. Untuk kelompok bilangan ( 10 , 24 , 26 ) diperoleh: 2 6 2 676 676 ​ = = = ​ 1 0 2 + 2 4 2 100 + 576 676 ​ Jadi, kelompok bilangan ( 10 , 24 , 26 ) merupakan tripel Pythagoras. Untukkelompok bilangan ( 15 , 36 , 39 ) diperoleh: 3 9 2 1.521 1.521 ​ = = = ​ 1 5 2 + 3 6 2 225 + 1.296 1.521 ​ Jadi, kelompok bilangan ( 15 , 36 , 39 ) merupakan tripel Pythagoras. Untukkelompok bilangan ( 20 , 48 , 52 ) diperoleh: 5 2 2 2.704 2.704 ​ = = = ​ 2 0 2 + 4 8 2 400 + 2.304 2.704 ​ Jadi, kelompok bilangan ( 20 , 48 , 52 ) merupakan tripel Pythagoras. Untukkelompok bilangan ( 25 , 60 , 65 ) diperoleh: 6 5 2 4.225 4.225 ​ = = = ​ 2 5 2 + 6 0 2 625 + 3600 4.225 ​ Jadi, kelompok bilangan ( 25 , 60 , 65 ) merupakan tripel Pythagoras. Untukkelompok bilangan ( 30 , 72 , 78 ) diperoleh: 7 8 2 6.084 6.084 ​ = = = ​ 3 0 2 + 7 2 2 900 + 5.184 6.084 ​ Jadi, kelompok bilangan ( 30 , 72 , 78 ) merupakan tripel Pythagoras. Tiga bilangan yang diperoleh di atas membentuk tripel Pythagoras. Dapat disimpulkan bahwa kelipatan dari tripel Pythagoras juga merupakan tripel Pythagoras. Dengan demikian, tigabilangan yang diperoleh membentuk tripel Pythagoras dankelipatan dari tripel Pythagoras juga merupakan tripel Pythagoras.