Iklan
Pertanyaan
Gambar 6.15 dibawah adalah gambar lingkaran dengan pusat E . Jari-jarinya 10 cm , ∠ AEN = 6 0 ∘ , JN adalah diameter dan ∠ JES = 9 0 ∘ , π = 3 , 14 . Tentukan: i. Besar ∠ JEA Besar ∠ AEN j. Besar ∠ JSA Besar ∠ ASN k. Panjang busur JA Panjang busur AN l. Luas juring JEA Luas juring AEN m. Apa hubungan antara i, j, k dan l?
Gambar 6.15 dibawah adalah gambar lingkaran dengan pusat . Jari-jarinya , , adalah diameter dan , .
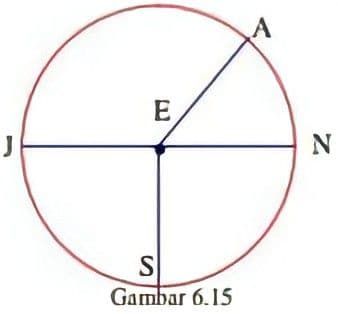
Tentukan:
i.
j.
k.
l.
m. Apa hubungan antara i, j, k dan l?
Iklan
SN
S. Nur
Master Teacher
Jawaban terverifikasi
5
5.0 (1 rating)
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia















