Diketahui sistem pertidaksamaan berikut! x + y 2 x + y ​ ≤ ≤ ​ 16 20 ​ a. Carilah titik perpotongan sumbu-x dan sumbu-y dari SPLDV(1) dan (2). b. Gambarlah grafiknya.

Pembahasan

Ingat kembali langkah-langkah menggambarkan daerah penyelesaian darisuatu sistem pertidaksamaan a x + b y ≤ c dan d x + ey ≤ f ,dengan a , b , c , d , e , f ∈ R : Gambar garis a x + b y = c dan d x + ey = f dengan mencari titik potong sumbu-x dan sumbu-y yang memenuhi masing-masing persamaan garis tersebut Cari titik potong kedua garis. Ambil sebarang titik uji ( x , y ) yang tidak melewati masing-masing garis tersebut. Subtitusikan titik uji ke masing-masingpertidaksamaan a x + b y ≤ c dan d x + ey ≤ f . Jika hasil subtitusi menghasilkan pernyataan yang benar, maka daerah di manatitik uji beradamerupakan daerah penyelesaian pertidaksamaan. Namun, jika menghasilkan pernyataan yang salah, maka daerah yang tidak terdapattitik uji merupakan daerah penyelesaian. Cari irisan dari daerah penyelesaian a x + b y ≤ c dan d x + ey ≤ f sehingga ditemukan daerah penyelesaian dari sistem pertidaksamaan tersebut. Oleh karena itu, akan dicari titik potong sumbu-x dan sumbu-y yang memenuhi masing-masing persamaan x + y = 16 dan 2 x + y = 20 , seperti berikut: Saat suatu titik memotong sumbu-x, maka y = 0 . Saat suatu titik memotong sumbu-y, maka x = 0 . Dengan mensubtitusikan y = 0 dan kemudian x = 0 ke x + y = 16 , diperoleh ​ ​ saat y = 0 : x + y = 16 x + 0 = 16 x = 16 0 + y = 16 y = 16 ​ ​ ​ ​ saat x = 0 : x + y = 16 ​ ​ Maka, titik potong sumbu-x dan sumbu-y untuk x + y = 16 , berturut-turut, adalah ( 16 , 0 ) dan ( 0 , 16 ) . Dengan menyubtitusikan y = 0 dan kemudian x = 0 ke 2 x + y = 20 , diperoleh ​ ​ saat y = 0 : 2 x + y = 20 2 x + 0 = 20 2 x = 20 x = 2 20 ​ x = 10 2 ( 0 ) + y = 20 0 + y = 20 y = 20 ​ ​ ​ ​ saat x = 0 : 2 x + y = 20 ​ ​ Maka, titik potong sumbu-x dan sumbu-y untuk 2 x + y = 20 , berturut-turut, adalah ( 10 , 0 ) dan ( 0 , 20 ) . Selanjutnya, titik potong kedua persamaan akan dicari seperti berikut: x + y = 16 2 x + y = 20 − x = − 4 x = 4 ​ ​ − ​ Subtitusikan x = 4 kesalahsatupersamaan, diperoleh x + y 4 + y y y ​ = = = = ​ 16 16 16 − 4 12 ​ ​ ​ Maka, titik potong garis x + y = 16 dan 2 x + y = 20 adalah ( 4 , 12 ) . 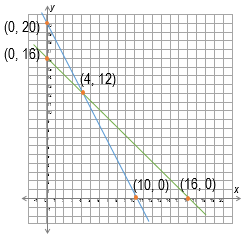Dengan menggambarkan titik-titikpotongdan menarik garis dari titik-titik tersebut pada koordinat kartesius, diperoleh gambar seperti berikut: Gambar 1 Selanjutnya, ambil titik uji ( 0 , 0 ) yang tidak berada pada kedua garis tersebut. 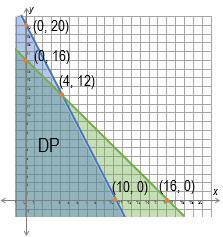Dengan mensubtitusikan titik tersebut ke masing-masing pertidaksamaan x + y ​ ≤ ​ 16 ​ dan 2 x + y ​ ≤ ​ 20 ​ , diperoleh x + y 2 x + y ​ = = ​ 0 + 0 = 0 ≤ 16 benar 2 ( 0 ) + 0 = 0 ≤ 20 benar ​ sehinggadaerah di mana titik ( 0 , 0 ) berada merupakan daerah penyelesaian kedua pertidaksamaan yang dapat digambarkan seperti berikut: Gambar 2 Dengan demikian, a) Titik perpotongan sumbu-x dan sumbu-y dari SPLDV di atas adalah ( 10 , 0 ) , ( 16 , 0 ) , ( 0 , 16 ) ,dan ( 0 , 20 ) . b) Gambar grafik daerah penyelesaian dari sistem pertidaksamaan dapat dilihatpada Gambar (2) di atas.