Pertanyaan

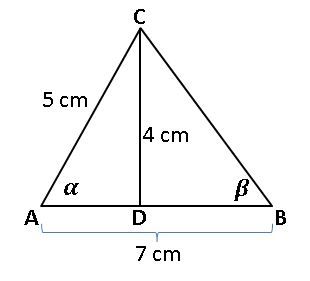
Diketahui segitiga ABC dengan panjang sisi AC = 5 cm dan panjang sisi AB = 7 cm . Titik D terletak pada sisi AB sehingga garis CD tegak lurus pada garis AB dengan panjang CD = 4 cm . Jika α menyatakan sudut BAC dan β menyatakan sudut ABC, tentukan nilai sin ( α + β ) + tan ( α − β ) .

Diketahui segitiga ABC dengan panjang sisi $AC = 5 cm$ dan panjang sisi $AB = 7 cm$ . Titik D terletak pada sisi AB sehingga garis CD tegak lurus pada garis AB dengan panjang $CD = 4 cm$ . Jika $α$ menyatakan sudut BAC dan $β$ menyatakan sudut ABC, tentukan nilai $sin (α + β) + tan (α - β)$ .

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

D. Rajib

Master Teacher

Mahasiswa/Alumni Universitas Muhammadiyah Malang

Jawaban terverifikasi

Jawaban

nilai sin ( α + β ) + tan ( α − β ) adalah 10 7 2 + 7 1 .

nilai

sin (α + β) + tan (α - β)

adalah

\frac{7}{10} 2 + \frac{1}{7}

Pembahasan

Iluastrasi segitiga ABC yang dimaksud pada soal adalah sebagai berikut: Sebelum menentukan perbandingan trigonometri, pertama perlu dicari terlebih dahulu panjangsetiap sisi dari segitiga ACD dan segitiga BCD. Panjang AD dapat diperoleh dari teorema pythagoras sebagai berikut: AD = = = = = AC 2 − CD 2 5 2 − 4 2 25 − 16 9 3 cm Panjang BD dapat diperoleh dari perhitungan berikut: BD = = = 7 − AD 7 − 3 4 cm Panjang BC dapat diperoleh dengan menggunakan teorema pythagoras sebagai berikut: BC = = = = = = CD 2 + BD 2 4 2 + 4 2 16 + 16 16 × 2 16 × 2 4 2 cm Ingat bahwa rumus perbandingan trigonometri untuk penjumlahan dua sudut bentuk sinus dan rumus perbandingan trigonometri untuk selisih dua sudut bentuk tangen adalah sebagai berikut: sin ( α + β ) = sin α ⋅ cos β + cos α ⋅ sin β tan ( α − β ) = 1 + tan α ⋅ tan β tan α − tan β Berdasarkan definisi sinus (perbandingan sisi), maka: sin α sin β = = = = = AC CD 5 4 BC CD 4 2 4 × 2 2 2 1 2 Berdasarkan definisi cosinus (perbandingan sisi), maka: cos α cos β = = = = = AC AD 5 3 BC BD 4 2 4 × 2 2 2 1 2 Berdasarkan definisi tangen (perbandingan sisi), maka: tan α tan β = = = = = AD CD 3 4 BD CD 4 4 1 Makanilai dari sin ( α + β ) + tan ( α − β ) , yaitu: = = = = = sin ( α + β ) + tan ( α − β ) sin α ⋅ cos β + cos α ⋅ sin β + 1 + t a n α ⋅ t a n β t a n α − t a n β 5 4 ⋅ 2 1 2 + 5 3 ⋅ 2 1 2 + 1 + 3 4 ⋅ 1 3 4 − 1 ( 5 4 + 5 3 ) 2 1 2 + 3 3 + 4 3 4 − 3 ( 5 7 ) 2 1 2 + 7 1 10 7 2 + 7 1 Dengan demikian, nilai sin ( α + β ) + tan ( α − β ) adalah 10 7 2 + 7 1 .

Iluastrasi segitiga ABC yang dimaksud pada soal adalah sebagai berikut:

Sebelum menentukan perbandingan trigonometri, pertama perlu dicari terlebih dahulu panjang setiap sisi dari segitiga ACD dan segitiga BCD. Panjang AD dapat diperoleh dari teorema pythagoras sebagai berikut:

$AD = = = = = AC^{2} - CD^{2} 5^{2} - 4^{2} 25 - 16 9 3 cm$

Panjang BD dapat diperoleh dari perhitungan berikut:

$BD = = = 7 - AD 7 - 3 4 cm$

Panjang BC dapat diperoleh dengan menggunakan teorema pythagoras sebagai berikut:

$BC = = = = = = CD^{2} + BD^{2} 4^{2} + 4^{2} 16 + 16 16 \times 2 16 \times 2 42 cm$

Ingat bahwa rumus perbandingan trigonometri untuk penjumlahan dua sudut bentuk sinus dan rumus perbandingan trigonometri untuk selisih dua sudut bentuk tangen adalah sebagai berikut:

$sin (α + β) = sin α \cdot cos β + cos α \cdot sin β tan (α - β) = \frac{tan α - tan β}{1 + tan α \cdot tan β}$

Berdasarkan definisi sinus (perbandingan sisi), maka:

$sin α sin β = = = = = \frac{CD}{AC} \frac{4}{5} \frac{CD}{BC} \frac{4}{4 2} \times \frac{2}{2} \frac{1}{2} 2$

Berdasarkan definisi cosinus (perbandingan sisi), maka:

$cos α cos β = = = = = \frac{AD}{AC} \frac{3}{5} \frac{BD}{BC} \frac{4}{4 2} \times \frac{2}{2} \frac{1}{2} 2$

Berdasarkan definisi tangen (perbandingan sisi), maka:

$tan α tan β = = = = = \frac{CD}{AD} \frac{4}{3} \frac{CD}{BD} \frac{4}{4} 1$

Maka nilai dari $sin (α + β) + tan (α - β)$ , yaitu:

$= = = = = sin (α + β) + tan (α - β) sin α \cdot cos β + cos α \cdot sin β + \frac{t a n α - t a n β}{1 + t a n α \cdot t a n β} \frac{4}{5} \cdot \frac{1}{2} 2 + \frac{3}{5} \cdot \frac{1}{2} 2 + \frac{\frac{4}{3} - 1}{1 + \frac{4}{3} \cdot 1} (\frac{4}{5} + \frac{3}{5}) \frac{1}{2} 2 + \frac{\frac{4 - 3}{3}}{\frac{3 + 4}{3}} (\frac{7}{5}) \frac{1}{2} 2 + \frac{1}{7} \frac{7}{10} 2 + \frac{1}{7}$