Pertanyaan

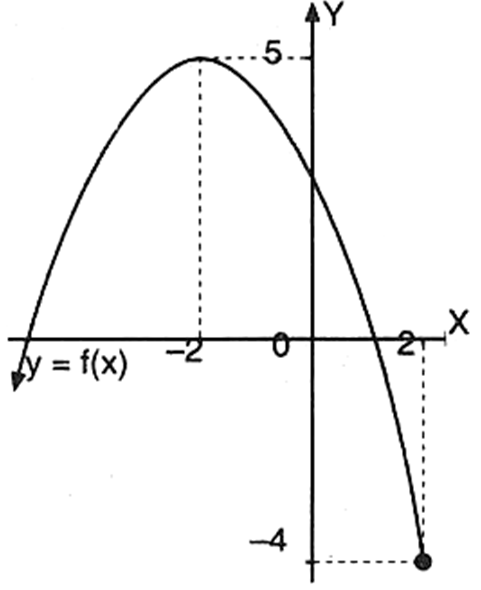
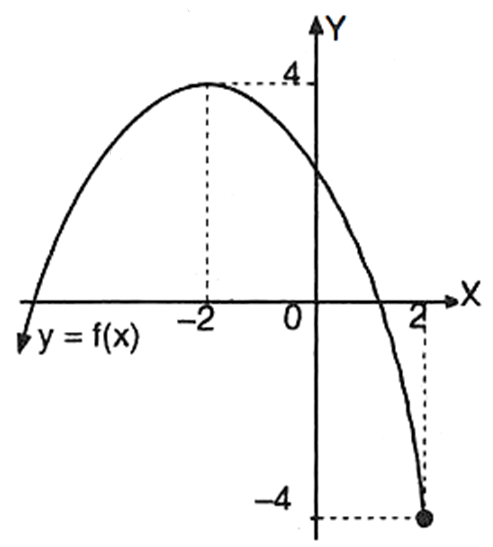
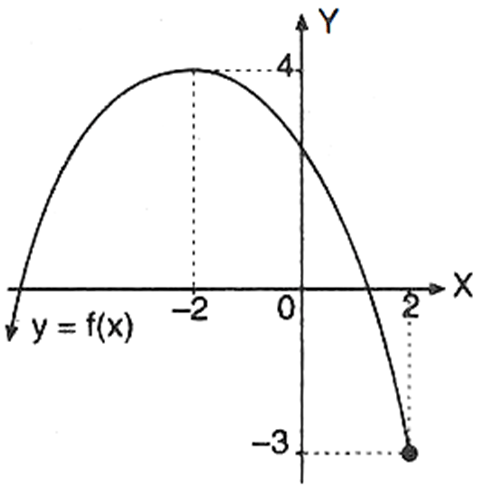
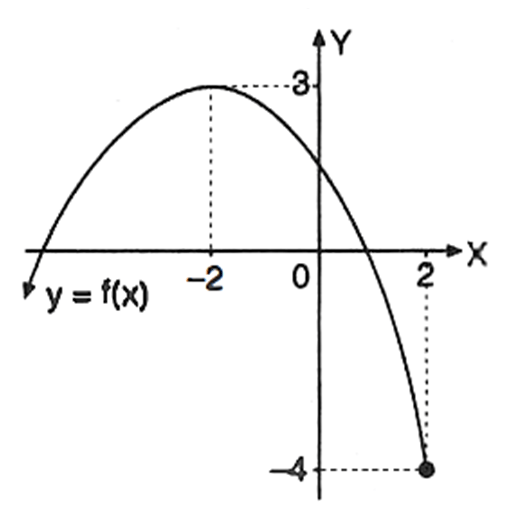
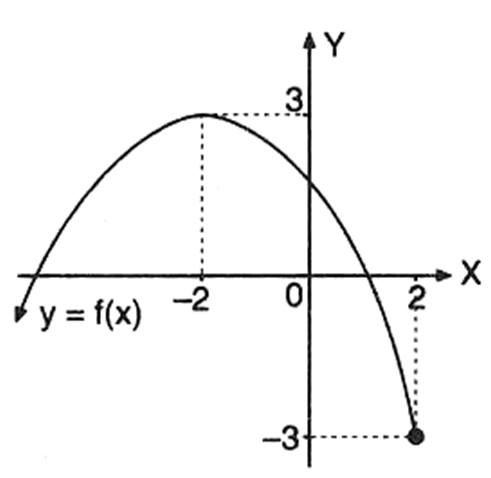
Diketahui f : x → − 2 1 x 2 − 2 x + 2. Jika daerah asal f adalah D f = { x ∣ x ≤ 2 , x ∈ R } , sketsa grafik fungsi y = f ( x ) adalah …

Diketahui $f : x \to - \frac{1}{2} x^{2} - 2 x + 2.$ Jika daerah asal $f$ adalah $D_{f} = {x ∣ x \leq 2, x \in R},$ sketsa grafik fungsi $y = f (x)$ adalah $\dots$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

S. Nur

Master Teacher

Jawaban terverifikasi

Jawaban

jawaban yang benar adalah B.

Pembahasan

Grafik fungsi kuadrat berbentuk parabola, maka untuk membuat sketsa grafik fungsi kuadrat harus ditentukan titik puncak dan titik koordinat dan sebagai berikut: Karena diketahui: , maka nilai pada saat adalah Sehingga, titik koordinat pada kartesius adalah Titik puncak dengan rumus: sebagai berikut: Karena maka nilai dan Sehingga, titik puncak dari fungsi tersebut adalah Koefisien pada fungsi bernilai negatif, maka grafik terbuka ke bawah. Berdasarkan uraian di atas, grafik fungsi memiliki titik ujung yaitu titik ,titik puncak grafik adalah titik , dan grafik terbuka ke bawah. Oleh karena itu, jawaban yang benar adalah B.

Grafik fungsi kuadrat berbentuk parabola, maka untuk membuat sketsa grafik fungsi kuadrat open parentheses y equals f left parenthesis x right parenthesis close parentheses harus ditentukan titik puncak dan titik koordinat dan sebagai berikut:

Karena diketahui: D subscript f equals open curly brackets right enclose x space x less or equal than 2 comma space x element of straight real numbers close curly brackets , maka nilai y equals f open parentheses x close parentheses pada saat x equals 2 adalah

Sehingga, titik koordinat open parentheses x comma space y close parentheses pada kartesius adalah open parentheses 2 comma negative 4 close parentheses.

Titik puncak dengan rumus: $open parentheses x subscript p comma space y subscript p close parentheses equals open parentheses negative fraction numerator b over denominator 2 a end fraction comma space minus fraction numerator b squared minus 4 a c over denominator 4 a end fraction close parentheses$ sebagai berikut:

Karena y equals f open parentheses x close parentheses equals negative 1 half x squared minus 2 x plus 2 comma maka nilai a equals negative 1 half comma b equals negative 2 dan c equals 2.

$table attributes columnalign right center left columnspacing 0px end attributes row cell open parentheses x subscript p comma space y subscript p close parentheses end cell equals cell open parentheses negative fraction numerator b over denominator 2 a end fraction comma space minus fraction numerator b squared minus 4 a c over denominator 4 a end fraction close parentheses end cell row blank equals cell open parentheses negative fraction numerator open parentheses negative 2 close parentheses over denominator open parentheses up diagonal strike 2 times negative begin display style fraction numerator 1 over denominator up diagonal strike 2 end fraction end style close parentheses end fraction comma space minus fraction numerator open parentheses negative 2 close parentheses squared minus 4 times open parentheses negative begin display style fraction numerator 1 over denominator up diagonal strike 2 end fraction end style close parentheses times up diagonal strike 2 over denominator open parentheses up diagonal strike 4 times negative begin display style fraction numerator 1 over denominator up diagonal strike 2 end fraction end style close parentheses end fraction close parentheses end cell row blank equals cell open parentheses negative fraction numerator open parentheses up diagonal strike minus 2 close parentheses over denominator open parentheses begin display style up diagonal strike minus 1 end style close parentheses end fraction comma space minus fraction numerator 4 minus 4 times open parentheses negative begin display style 1 end style close parentheses over denominator open parentheses negative begin display style 2 end style close parentheses end fraction close parentheses end cell row blank equals cell open parentheses negative 2 over 1 comma space minus open parentheses negative fraction numerator 4 plus 4 over denominator 2 end fraction close parentheses close parentheses end cell row blank equals cell open parentheses negative 2 comma space 8 over 2 close parentheses end cell row cell open parentheses x subscript p comma space y subscript p close parentheses end cell equals cell open parentheses negative 2 comma space 4 close parentheses end cell end table$

Sehingga, titik puncak dari fungsi tersebut adalah table attributes columnalign right center left columnspacing 0px end attributes row cell open parentheses x subscript p comma space y subscript p close parentheses end cell equals cell open parentheses negative 2 comma space 4 close parentheses. end cell end table

Koefisien x squared pada fungsi y equals f open parentheses x close parentheses equals negative 1 half x squared minus 2 x plus 2 bernilai negatif, maka grafik terbuka ke bawah.

Berdasarkan uraian di atas, grafik fungsi f open parentheses x close parentheses equals negative 1 half x squared minus 2 x plus 2 memiliki titik ujung yaitu titik open parentheses 2 comma negative 4 close parentheses , titik puncak grafik adalah titik open parentheses negative 2 comma 4 close parentheses , dan grafik terbuka ke bawah.

Oleh karena itu, jawaban yang benar adalah B.