Pertanyaan

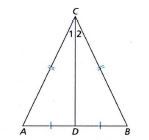
Diketahui △ ABC dengan A C = BC dan AD = BD . Buktikan bahwa: △ ACD ≅ △ BCD , ∠ A = ∠ B , dan ∠ C 1 = ∠ C 2 .

Diketahui $△ ABC$ dengan $A C = BC$ dan $AD = BD$ .

Buktikan bahwa: $△ ACD ≅ △ BCD$ , $∠ A = ∠ B$ , dan $∠ C_{1} = ∠ C_{2}$ . $\;$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

E. Lestari

Master Teacher

Mahasiswa/Alumni Universitas Sebelas Maret

Jawaban terverifikasi

Jawaban

terbukti △ ACD ≅ △ BCD , ∠ A = ∠ B , dan ∠ C 1 = ∠ C 2 .

terbukti

△ ACD ≅ △ BCD

∠ A = ∠ B

, dan

∠ C_{1} = ∠ C_{2}

. $\;$

Pembahasan

Jawaban yang benar untuuk pertanyaan tersebut adalah △ ACD ≅ △ BCD , ∠ A = ∠ B , dan ∠ C 1 = ∠ C 2 terbukti benar. Kekongruenan pada Segitiga Untuk membuktikan sisi-sisi sama panjang san sudut-sudut sama besar secara deduktif, buktikan terlebih dahulu segitiga-segitiga yang memuat sisi-sisi dan/atau sudut-sudut tersebut kongruen. Sebagai konsekuensinya, berlaku prinsip kongruensi DSSPSSB (di depan sisi sama panjang terdapat sudut sama besar), dan DSSBSSP (di depan sudut sama besar terdapat sisi sama panjang). Langkah-langkah pembuktian △ ACD ≅ △ BCD , ∠ A = ∠ B , dan ∠ C 1 = ∠ C 2 . 1. Sisi A C = BC (diketahui) 2. Sisi AD = BD (diketahui) 3. Sisi CD = CD Sisi saling berimpit sama panjang. 4. △ ACD ≅ △ BCD Aksioma kongruensi 1: Dua segitiga kongruen jika ketiga sisi yang bersesuaian sama panjang. 5. ∠ A = ∠ B Prinsip kongruensi:DSSPSSB (di depan sisi sama panjang terdapat sudut sama besar). ∠ A menghadap sisi CD , sedangkan ∠ B menghadap sisi CD . 6. ∠ C 1 = ∠ C 2 Prinsip kongruensi:DSSPSSB (di depan sisi sama panjang terdapat sudut sama besar). ∠ C 1 menghadap sisi AD , sedangkan ∠ C 2 menghadap sisi BD . Dengan demikian, terbukti △ ACD ≅ △ BCD , ∠ A = ∠ B , dan ∠ C 1 = ∠ C 2 .

Jawaban yang benar untuuk pertanyaan tersebut adalah $△ ACD ≅ △ BCD$ , $∠ A = ∠ B$ , dan $∠ C_{1} = ∠ C_{2}$ terbukti benar.

Kekongruenan pada Segitiga

Untuk membuktikan sisi-sisi sama panjang san sudut-sudut sama besar secara deduktif, buktikan terlebih dahulu segitiga-segitiga yang memuat sisi-sisi dan/atau sudut-sudut tersebut kongruen. Sebagai konsekuensinya, berlaku prinsip kongruensi DSSPSSB (di depan sisi sama panjang terdapat sudut sama besar), dan DSSBSSP (di depan sudut sama besar terdapat sisi sama panjang).

Langkah-langkah pembuktian $△ ACD ≅ △ BCD$ , $∠ A = ∠ B$ , dan $∠ C_{1} = ∠ C_{2}$ . $\;$