Diketahui f ( x ) = 4 x dan g ( x ) = 4 − x . Kemudian, perhatikan beberapa pernyataan berikut ini. (i) Grafik f ( x ) dan grafik g ( x ) berpotongan di titik ( 0 , 1 ) . (ii) Grafik g ( x ) adalah cermin grafik f ( x ) terhadap sumbu- y . (iv) Fungsi f ( x ) dan g ( x ) memiliki domain dan range yang sama. (iii) Grafik f ( x ) turun sedangkangrafik g ( x ) naik untuk semua nilai x ∈ R . Pernyataan yang BENARditunjukkan olehnomor ….

Pembahasan

Diketahui f ( x ) = 4 x dan g ( x ) = 4 − x . Untuk mengetahui mana pernyataan yang benar, maka cek kebenaran setiap pernyataan. Pernyataan (i) Grafik f ( x ) dan grafik g ( x ) berpotongan di titik ( 0 , 1 ) . Untuk mengetahui kebenaran pernyataan (i), terdapat dua cara penyelesaian. Cara pertama: Untuk mengetahui perpotongan kedua grafik eksponen tersebut, perhatikan perhitungan pada persamaan berikut ini. f ( x ) 4 x ​ = = ​ g ( x ) 4 − x ​ Karena bilangan pokok persamaan di atas sudah sama, yakni 4. Akibatnya, pangkat keduanya haruslah sama sehingga didapat hubungan berikut ini. x x + x 2 x x ​ = = = = ​ − x 0 0 0 ​ Kemudian, substitusi x = 0 ke salah satu fungsi tersebut (misalnya fungsi f ( x ) ) untuk memperoleh ordinat y. f ( x ) y y ​ = = = ​ 4 x 4 0 1 ​ Dari perhitungan di atas, dapat disumpulkan bahwa titik potong kedua grafik eksponen tersebut adalah ( 0 , 1 ) . Oleh karena itu, pernyataan (i) bernilai BENAR. Cara kedua: Jika kamu kesulitan menggunakan cara pertama, maka gunakan cek posisi titik tersebut pada masing-masing grafik dengan cara substitusi. Agar lebih mudah mengetahui apakah titik potong kedua grafik tersebut adalah ( 0 , 1 ) , maka substitusika x = 0 ke setiap fungsi tersebut.Perhatikan perhitungan berikut ini! f ( x ) = 4 x f ( 0 ) = 4 0 f ( 0 ) = 1 Akibatnya, grafik f ( x ) melalui ( 0 , 1 ) . g ( x ) = 4 − x g ( 0 ) = 4 − 0 g ( 0 ) = 4 0 g ( 0 ) = 1 Akibatnya, grafik g ( x ) melalui ( 0 , 1 ) . Karena kedua grafik sama-sama melalui titik ( 0 , 1 ) , maka dapat disimpulkan bahwa kedua grafik eksponen tersebut berpotongan di titik ( 0 , 1 ) . Oleh karena itu, pernyataan (i) bernilai BENAR. Pernyataan (ii) Grafik g ( x ) adalah cermin grafik f ( x ) terhadap sumbu- y . Untuk mengetahui pernyataan (iii) benar atau tidak, maka gambarkan kedua grafik tersebut dalam satu diagram kartesius dengan cara membuat tabel berikut ini. 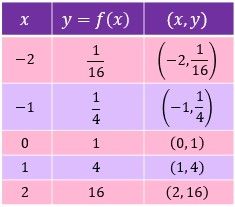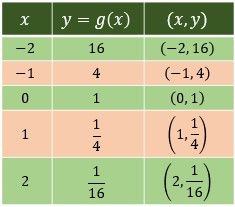Tabel grafik f ( x ) Tabel grafik g ( x ) Dari kedua tabel di atas, gambarkan kedua grafik pada diagram kartesius berikut ini. 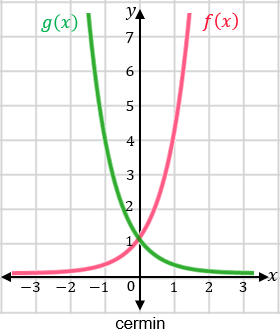Ingat kembali konsep pencerminan (refleksi) bahwa jarak benda ke cermin akan sama dengan jarak cermin ke bayangan benda tersebut . Pada interval 1 < y < ∞ , jarak setiap titikpada grafik f ( x ) kesumbu- y sama dengan jarak sumbu- y ke setiap titik g ( x ) . Begitupun pada interval 0 < y < 1 ,jarak setiap titikpada grafik f ( x ) kesumbu- y sama dengan jarak sumbu- y ke setiap titik g ( x ) . Akibatnya, grafik g ( x ) adalah cermin grafik f ( x ) dengansumbu- y sebagai cerminnya. Oleh karena itu, pernyataan (ii) adalah pernyataan yang BENAR. Pernyataan (iii) Fungsi f ( x ) dan g ( x ) memiliki domain dan range yang sama. Dari grafik pada pernyataan (ii), grafik f ( x ) dan g ( x ) terdefinisi untuk semua x anggota bilangan real. Akibatnya, diperoleh bahwa domain kedua fungsi tersebut sama, yakni { x ∣ x ∈ R } . Kemudian, nilai y pada grafik f ( x ) dan g ( x ) hanya terdefinisi pada interval 0 < y < ∞ . Akibatnya, diperoleh bahwa range kedua fungsitersebut sama, yakni { y ∣ y > 0 , y ∈ R } . Oleh karena itu, pernyataan (iii) adalah pernyataan yang BENAR. Pernyataan (iv) Grafik f ( x ) turun sedangkangrafik g ( x ) naik untuk semua nilai x ∈ R . Dari grafik pada pernyataan (ii), terlihat bahwa grafik f ( x ) naik sedangkan grafik g ( x ) turun. Oleh karena itu, pernyataan (iv) adalah pernyataan yang SALAH. Dengan demikian, pernyataan yang bernilai BENAR adalah pernyataan(i), (ii) dan (iii) saja. Jadi, jawaban yang tepat adalah D.