Diketahui bahwakubus ABCD.EFGH memiliki panjang rusuk 4 cm . Titik P berada di tengah ruas garis EH dan titik Q berada di tengah ruas garis CD. Tangen sudut antara garis AP dan BQ adalah ....

Pembahasan

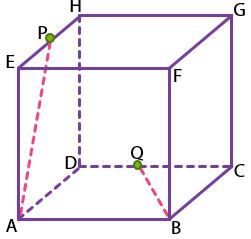
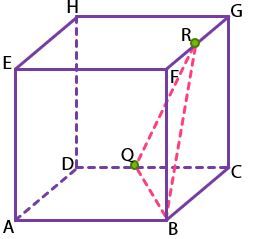
Perhatikan gambar berikut! Dapat diperhatikan bahwa AP dan BQ adalah dua garis yang saling bersilangan. Untuk mencari besar sudut antara keduanya, geser salah satu garis, dalam hal ini geser AP sehingga menjadi garis BR, dengan R berada di tengah ruas garis FG seperti berikut. Dapat diperhatikan bahwa terbentuk segitiga BQR. Kemudian, panjang BQ dan panjang BR dapat dihitung menggunakan Teorema Pythagoras dengan memperhatikan segitiga BFR sebagai berikut. Dengan cara yang sama, diperoleh . Kemudian, untuk menghitung panjang QR, kita dapat menggunakan Teorema Pythagoras pada segitiga QSR. Namun, sebelum menghitung panjang QR, kita perlu mengetahui panjang QS terlebih dahulu. 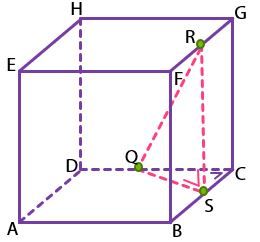Ingat bahwa dan . Kemudian, perhatikan segitiga QCS siku-siku di C! . Ingat bahwa . Oleh karena itu, kita dapat menghitung panjang QR dengan memerhatikan segitiga QSR siku-siku di S sebagai berikut. Selanjutnya, akan dicari tangen sudut antara AP dengan BQ, yang berarti sama dengan tangen sudut antara BQ dengan BR, yaitu Oleh karena itu, perhatikan segitiga QBR berikut! 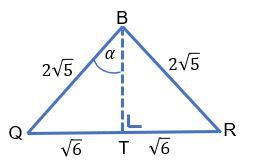Dapat diperhatikan bahwa segitiga BQR adalah segitiga sama kaki dengan panjang BQ sama dengan panjang BR. Oleh karena itu, jika digambarkan garis tinggi BT, maka BT juga merupakan garis berat sehingga T membagi QR menjadi dua bagian yang sama panjang. Selanjutnya, dapat diperhatikan bahwa panjang BT dapat kita hitung dengan cara sebagai berikut. Didapat sehingga tangen sudut antara BQ dengan BR adalah sebagai berikut. Jadi, jawaban yang tepat adalah B.