Pertanyaan

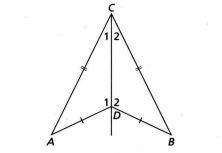
Diketahui ABCD adalah layang-layang gantole dengan AC = BC dan AD = BD . Buktikan bahwa: △ ACD ≅ △ BCD , ∠ A = ∠ B , ∠ C 1 = ∠ C 2 , dan ∠ D 1 = ∠ D 2 .

Diketahui $ABCD$ adalah layang-layang gantole dengan $AC = BC$ dan $AD = BD$ .

Buktikan bahwa: $△ ACD ≅ △ BCD$ , $∠ A = ∠ B$ , $∠ C_{1} = ∠ C_{2}$ , dan $∠ D_{1} = ∠ D_{2}$ . $\;$

S. Nur

Master Teacher

Jawaban terverifikasi

Jawaban

terbukti △ ACD ≅ △ BCD , ∠ A = ∠ B , ∠ C 1 = ∠ C 2 , dan ∠ D 1 = ∠ D 2 .

terbukti

△ ACD ≅ △ BCD

∠ A = ∠ B

∠ C_{1} = ∠ C_{2}

, dan

∠ D_{1} = ∠ D_{2}

. $\;$

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah terbukti △ ACD ≅ △ BCD , ∠ A = ∠ B , ∠ C 1 = ∠ C 2 , dan ∠ D 1 = ∠ D 2 . Kekongruenan pada Segitiga Untuk membuktikan sisi-sisi sama panjang dan sudut-sudut sama besar secara deduktif, buktikan terlebih dahulu segitiga-segituga yang memuat sisi-sisi dan/atau sudut-sudut tersebut kongruen. Sebagai konsekuensinya, berlaku prinsip kongruensi DSSPSSB (di depan sisi sama panjang terdapat sudut sama besar) dan DSSBSSP (di depan sudut sama besar terdapat sisi sama panjang). Langkah pembuktian △ ACD ≅ △ BCD , ∠ A = ∠ B , ∠ C 1 = ∠ C 2 , dan ∠ D 1 = ∠ D 2 . 1. Sisi AC = BC (diketahui) 2. Sisi AD = BD (diketahui) 3. Sisi CD = CD (diketahui) Sisi yang berimpit sama panjang. 4. △ ACD ≅ △ BCD Aksioma kongruensi 1: Dua segitiga kongruen jika ketiga sisi yang bersesuaian sama panjang. 5. ∠ C 1 = ∠ C 2 Prinsip kongruensi: DSSPSSB (di depan sisi sama panjang terdapat sudut sama besar). ∠ C 1 menghadap sisi AD , sedangkan ∠ C 2 menghadap sisi BD . 6. ∠ D 1 = ∠ D 2 Prinsip kongruensi: DSSPSSB (di depan sisi sama panjang terdapat sudut sama besar). ∠ D 1 menghadap sisi AC sedangkan ∠ D 2 menghadap sisi BC . Dengan demikian, terbukti △ ACD ≅ △ BCD , ∠ A = ∠ B , ∠ C 1 = ∠ C 2 , dan ∠ D 1 = ∠ D 2 .

Jawaban yang benar untuk pertanyaan tersebut adalah terbukti $△ ACD ≅ △ BCD$ , $∠ A = ∠ B$ , $∠ C_{1} = ∠ C_{2}$ , dan $∠ D_{1} = ∠ D_{2}$ .

Kekongruenan pada Segitiga

Untuk membuktikan sisi-sisi sama panjang dan sudut-sudut sama besar secara deduktif, buktikan terlebih dahulu segitiga-segituga yang memuat sisi-sisi dan/atau sudut-sudut tersebut kongruen. Sebagai konsekuensinya, berlaku prinsip kongruensi DSSPSSB (di depan sisi sama panjang terdapat sudut sama besar) dan DSSBSSP (di depan sudut sama besar terdapat sisi sama panjang).

Langkah pembuktian $△ ACD ≅ △ BCD$ , $∠ A = ∠ B$ , $∠ C_{1} = ∠ C_{2}$ , dan $∠ D_{1} = ∠ D_{2}$ . $\;$

1. Sisi $AC = BC$ (diketahui)

2. Sisi $AD = BD$ (diketahui)

3. Sisi $CD = CD$ (diketahui)

Sisi yang berimpit sama panjang.

4. $△ ACD ≅ △ BCD$

Aksioma kongruensi 1: Dua segitiga kongruen jika ketiga sisi yang bersesuaian sama panjang.

5. $∠ C_{1} = ∠ C_{2}$

Prinsip kongruensi: DSSPSSB (di depan sisi sama panjang terdapat sudut sama besar).

$∠ C_{1}$ menghadap sisi $AD$ , sedangkan $∠ C_{2}$ menghadap sisi $BD$ .

6. $∠ D_{1} = ∠ D_{2}$

Prinsip kongruensi: DSSPSSB (di depan sisi sama panjang terdapat sudut sama besar).

$∠ D_{1}$ menghadap sisi $AC$ sedangkan $∠ D_{2}$ menghadap sisi $BC$ .

Dengan demikian, terbukti $△ ACD ≅ △ BCD$ , $∠ A = ∠ B$ , $∠ C_{1} = ∠ C_{2}$ , dan $∠ D_{1} = ∠ D_{2}$ . $\;$

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.0 (4 rating)

Dasha

Pembahasan lengkap banget Mudah dimengerti Bantu banget Makasih ❤️

Satrio Djati

Pembahasan lengkap banget

fahmi khakim

Makasih ❤️ Pembahasan lengkap banget dan Mudah dimengerti

Pertanyaan serupa

△ ABC kongruen dengan △ BDE , dengan AB = BE . Besar ∠ ABC adalah ... derajat.

5.0

Jawaban terverifikasi

Diketahui △ KLM kongruen dengan △ PQR . Apabila besar ∠ K = ( 3 x + 7 ) ∘ , ∠ P = ( 2 x + 24 ) ∘ , ∠ L = ( 5 x − 42 ) ∘ , dan ∠ Q = ( 4 x − 25 ) ∘ , ∠ R = ....

4.6

Jawaban terverifikasi

Diketahui trapesium ABC dan trapesium DEF pada gambar di bawah ini adalah kongruen. a. Pasangan sisi yang bersesuaian beserta panjang sisinya.

0.0

Jawaban terverifikasi

Pada gambar berikut. a. Buktikan △ ABC dan △ QPR kongruen.

5.0

Jawaban terverifikasi

Perhatikan gambar segitiga siku-siku berikut. Diketahui BD adalah garis bagi dan DE ⊥ BC . Tentukan: b. pasangan sudut yang sama panjang,

5.0

Jawaban terverifikasi