Diberikan domain dari fungsi f − g : R → R adalah D f − g ​ = { x ∣ a < x ≤ b atau c ≤ x < d , x ∈ R } , dengan , b , ,dan d adalah bilangan real. Diketahui f ( x ) = 5 2 x 2 − 8 ​ ​ g ( x ) = − x 2 + 25 ​ 15 x 3 − 81 ​ Nilai ( f − g ) ( x ) yang mungkin terdefinisiadalah ....

Pembahasan

Ingat kembali bahwa jika domain dari fungsi dan secara berturut-turut adalah dan , maka domain dari fungsi adalah . Oleh karena itu, akan dicari dan terlebih dahulu. Perhatikan bahwa adalah fungsi dalam bentuk pecahan. Terdapat bentuk akar sebagai pembilang. Artinya, syarat pada domain didapat dengan cara membuat bentuk di dalam akar positif atau nol. Perhatikan bahwa pembuat nolnya adalah sebagai berikut. ( x + 2 ) ( x − 2 ) x = − 2 atau x ​ = = ​ 0 2 ​ Diperoleh garis bilangan sebagai berikut. 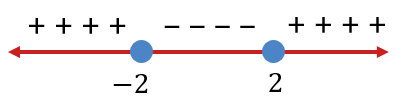Karena tanda pada pertidaksamaan adalah , maka diambil daerah yang bernilai positif, yaitu atau . Oleh karena itu, didapat . Kemudian, perhatikan bahwa adalah fungsi dalam bentuk pecahan. Terdapat bentuk akar sebagai penyebut. Artinya, syarat pada domain didapat dengan cara membuat bentuk di dalam akar positif. Perhatikan bahwa pembuat nolnya adalah sebagai berikut. ( x + 5 ) ( x − 5 ) x = − 5 atau x ​ = = ​ 0 5 ​ Diperoleh garis bilangan sebagai berikut. 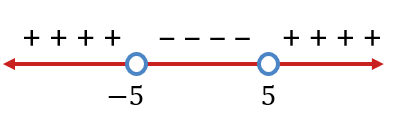Karena tanda pada pertidaksamaan adalah , maka diambil daerah yang bernilai negatif, yaitu . Oleh karena itu, didapat . Perhatikan bahwa dan . Akibatnya,didapat irisannya dalamgaris bilangan sebagai berikut. Diperoleh D f − g ​ = { x ∣ − 5 < x ≤ − 2 atau 2 ≤ x < 5 , x ∈ R } . Diketahui pada soal bahwa D f − g ​ = { x ∣ a < x ≤ b atau c ≤ x < d , x ∈ R } . Akibatnya, didapat nilai a = − 5 , b = − 2 , c = 2 , dan . Selanjutnya, perhatikan perhitunganberdasarkan bentuk yang tersedia padapilihan jawaban berikut! A . − b a ​ = − ( − 2 ) ( − 5 ) ​ = − 2 5 ​ B . − b a 2 ​ = − ( − 2 ) ( − 5 ) 2 ​ = 2 25 ​ C . b c ​ = ( − 2 ) 2 ​ = − 1 D . a d ​ = ( − 5 ) 5 ​ = − 1 E . b c ​ − a d ​ = − 1 − ( − 1 ) = 0 ​ Dapat diperhatikan bahwa nilai ( f − g ) ( x ) yang memungkinkan adalah saat . Karena nilai merupakananggota dari domain dari D f − g ​ = { x ∣ a < x ≤ b atau c ≤ x < d , x ∈ R } . Sedangkan nilai x yang laintidak terdefinisi pada domain. Jadi, jawaban yang tepat adalah A.