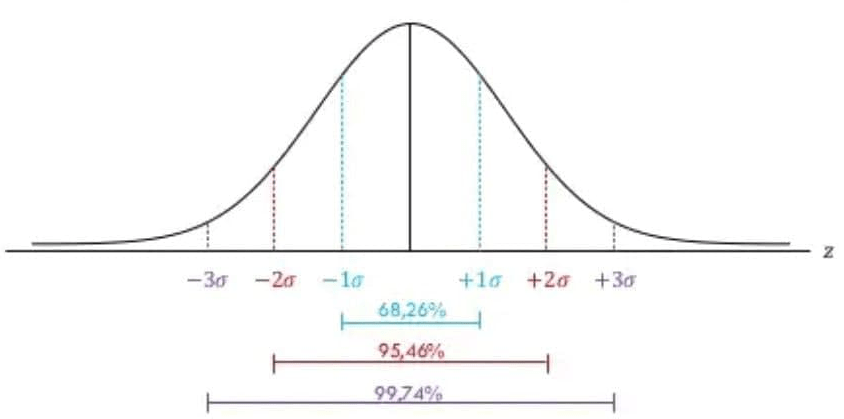
30 anak-anak mendapatkan total 2.700 kartu kasti. Jika 16% -nya memiliki kurang dari 70 kartu kasti dan banyaknya kartu kasti per anak memiliki distribusi normal, berapa persen dari anak-anak tersebut yang memiliki lebih dari 130 kartu kasti?

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah A. Perhatikan kurva distribusi normal berikut. Beberapa bagian luas di bawah kurva untuk distribusi normal adalah sebagai berikut. 1. Kira-kira 68 , 27% dari kasus ada dalam daerah satu simpangan baku sekitar rata-rata, yaitu antara μ − σ dan μ + σ ; 2. kira-kira 95 , 45% dari kasus ada dalam daerah satu simpangan baku sekitar rata-rata, yaitu antara μ − 2 σ dan μ + 2 σ ; 3. kira-kira 95 , 45% dari kasus ada dalam daerah satu simpangan baku sekitar rata-rata, yaitu antara μ − 3 σ dan μ + 3 σ ; 4. sekalipun secara teoretis ujung kurva normal ke kanan dan ke kiri tak berhingga jauhnya, namun praktis dalam jarak lebih dari tiga simpangan baku dari rata-rata ( μ ± 3 σ ) luas kurva normal itu tidak berarti lagi (kurang dari 1% ) Diketahui data berdistribusi normal sehingga kita mempunyai petunjuk bahwa soal ini berkaitan dengan rata rata ( μ ) dan simpangan baku ( σ ) . Cari rata-rata μ ​ = = = ​ jumlah anak jumlah kartu kasti ​ 30 2.700 ​ 90 ​ Cari simpangan baku Diketahui bahwa 16% dari jumlah anak memiliki 70 kartu kasti, sehingga kita bisa temukan Z dengan mencari nilai yang mendekati 16% atau 1 , 6 pada tabel distribusi normal dan akan diperoleh Z = − 1 z − 1 σ ​ = = = ​ σ x − μ ​ σ 70 − 90 ​ 20 ​ Cari persentase Persentase anak memiliki lebih dari 130 kartu kasti bisa kita peroleh dengan mencari Z terlebih dahulu. z ​ = = = = ​ σ x − μ ​ 20 130 − 90 ​ 20 40 ​ 2 ​ Diperoleh nilai z = 2 yang artinya ada dalam daerah antara 0 dan μ + 2 σ . Luas kurva pada daerah tersebut, yaitu 0 , 9545 ÷ 2 = 0 , 47725 . Karena kurva simetris, luas kurva di sebelah kanan 0 adalah 0 , 5 sehingga diperoleh: P ( Z ≥ x ) ​ = = ​ 0 , 5 − 0 , 47725 0 , 02275 ​ Persentase banyak anak yang memiliki lebih dari 130 kartu kastiadalah: Persentase ​ = = ≈ ​ 0 , 02275 × 100% 2 , 275% 2% ​ Oleh karena itu, jawaban yang tepat adalah A.