HA
Haddad A

11 Desember 2025 16:44
Iklan
HA
Haddad A

11 Desember 2025 16:44
Pertanyaan
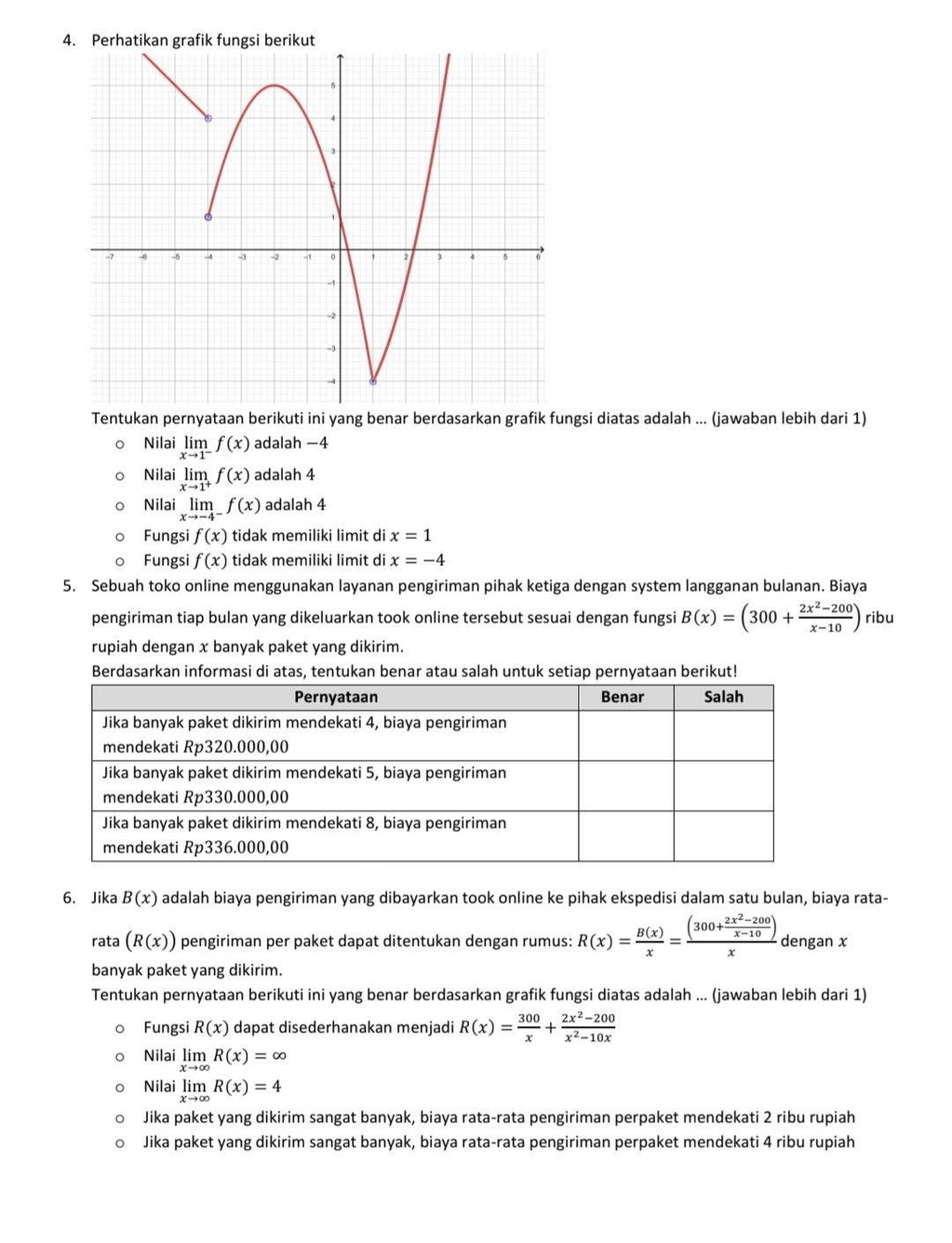
Mohon bantuannya
Mohon bantuannya

33
1
Iklan
PA
P. Anindya
Mahasiswa/Alumni Universitas Negeri Yogyakarta
12 Desember 2025 01:15
Jawaban terverifikasi
4) Benar: lim x→1− f(x) = 4; f(x) tidak memiliki limit di x = 1; f(x) tidak memiliki limit di x = −4 5) Salah, Benar, Benar 6) Benar: R(x) dapat disederhanakan seperti yang diberikan; rata-rata mendekati 2 ribu rupiah. Salah: lim x→∞ R(x) = ∞; lim x→∞ R(x) = 4; rata-rata mendekati 4 ribu rupiah 3) Salah, Benar, Benar Penjelasan Pada grafik soal 4, saat x mendekati 1 dari kiri nilai f(x) mendekati 4, sedangkan dari kanan mendekati nilai minimum tajam di bawah −4, sehingga limit dua arah di x = 1 tidak ada; di x = −4 tampak ketakselanjaran loncat (titik terbuka dan nilai dari sisi kanan berbeda), sehingga limit juga tidak ada. Pada soal 5, fungsi biaya B(x) dapat disederhanakan sehingga menjadi linear untuk x ≠ 10, lalu nilai batas di 4, 5, dan 8 dihitung langsung. Pada soal 6, rata-rata per paket R(x) menyederhana ke 2 + 320/x sehingga saat x sangat besar mendekati 2 ribu rupiah; bentuk pecahan yang diberikan setara, sedangkan klaim limit 4 atau tak hingga salah. Pada soal 3, jari-jari sama dengan jarak pusat ke garis, menghasilkan 2√10 (bukan 2√2), persamaan lingkaran benar, dan titik (0, −1) berada pada garis sekaligus memenuhi persamaan lingkaran sehingga menjadi titik singgung. Penjabaran ekspresi matematika - Soal 5: B(x) = 300 + (2x^2 − 200)/(x − 10) = 300 + 2(x − 10)(x + 10)/(x − 10) = 300 + 2(x + 10) = 2x + 320 (ribu), x ≠ 10. • x→4: 2(4)+320 = 328 → Salah pernyataan 1. • x→5: 2(5)+320 = 330 → Benar pernyataan 2. • x→8: 2(8)+320 = 336 → Benar pernyataan 3. - Soal 6: R(x) = B(x)/x = 300/x + (2x^2 − 200)/(x(x − 10)) = 300/x + (2x^2 − 200)/(x^2 − 10x) = (2x + 320)/x = 2 + 320/x. • lim x→∞ R(x) = 2 (ribu) → klaim “∞” dan “4” salah; rata-rata mendekati 2 ribu benar, 4 ribu salah. - Soal 3: r = jarak pusat ke garis = |(−2) − 3(5) − 3|/√(1^2 + (−3)^2) = |−20|/√10 = 2√10. • Lingkaran: (x + 2)^2 + (y − 5)^2 = (2√10)^2 = 40 → x^2 + y^2 + 4x − 10y − 11 = 0. • Uji (0, −1): pada garis 0 − 3(−1) − 3 = 0; pada lingkaran 2^2 + (−6)^2 = 4 + 36 = 40 → titik persekutuan benar.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



