AMBUS A
22 Februari 2023 04:58
Iklan
AMBUS A
22 Februari 2023 04:58
Pertanyaan
Fungsi f(x, y) =cx+ 4y dengan kendala: 2x +y ≥ 10, x+2y≥ 8, x≥ 0, dan y ≥ 0 mencapai minimum di (4,2) , jika... (A) c≤-8 atau c≥2 (B) c≤2 atau c≥8 (C) - 2≤ c≤ 8 (D)2≤c≤8 (E)2≤c≤I0
Fungsi f(x, y) =cx+ 4y dengan kendala: 2x +y ≥ 10, x+2y≥ 8, x≥ 0, dan y ≥ 0 mencapai minimum di (4,2) , jika...
(A) c≤-8 atau c≥2
(B) c≤2 atau c≥8
(C) - 2≤ c≤ 8
(D)2≤c≤8
(E)2≤c≤I0
2
2
Iklan
Ren R
23 Februari 2023 00:05
<p>Jawaban: D.</p><p> </p><p>Supaya fungsi f(x, y) = cx+ 4y dengan kendala 2x + y ≥ 10, x + 2y ≥ 8, x ≥ 0, dan y ≥ 0 mencapai minimum di titik (4, 2), maka konstanta c memenuhi:</p><p> </p><ul><li>Garis 2x + y = 10 melalui tiitk (5,0) dan (0,10) dan daerah penyelesaian 2x +y ≥ 10 berada di atas garis 2x + y = 10.</li><li>Garis 2x + y = 8 melalui titik (8,0) dan (0,4) dan daerah penyelesaian x+2y ≥ 8 berada di atas garis x + 2y = 8.</li><li>Daerah penyelesaian x ≥ 0 berada di kanan sumbu Y<i>.</i></li><li>Daerah penyelesaian y ≥ 0 berada di atas garis sumbu X<i>.</i></li></ul><p> </p><p>Daerah penyelesaian terlampir</p><p> </p><p>Titik pojok (4,2), (8,0), dan (0,10) disubstitusikan.</p><p> </p><ul><li>f(4, 2) = 4c + 8</li><li>f(8, 0) = 8c</li><li>f(0, 10) = 40</li></ul><p> </p><p>Agar (4,2) menjadi titik minimum maka:</p><p> </p><p>4c + 8 ≤ 8c</p><p>8 ≤ 4c</p><p>2 ≤ c</p><p> </p><p>dan</p><p> </p><p>4c + 8 ≤ 40</p><p>4c ≤ 32</p><p>c ≤ 8</p><p> </p><p>Sehingga dapat dituliskan:</p><p> </p><p>2 ≤ c ≤ 8 (Pilihan Jawaban D).</p>
Jawaban: D.
Supaya fungsi f(x, y) = cx+ 4y dengan kendala 2x + y ≥ 10, x + 2y ≥ 8, x ≥ 0, dan y ≥ 0 mencapai minimum di titik (4, 2), maka konstanta c memenuhi:
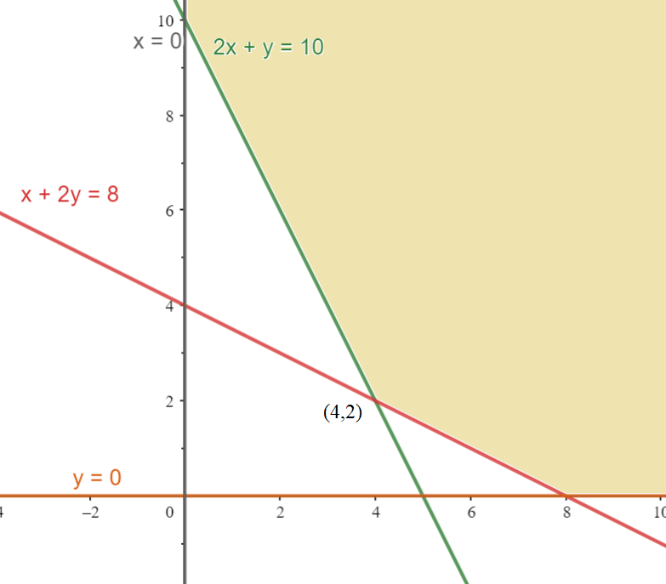
- Garis 2x + y = 10 melalui tiitk (5,0) dan (0,10) dan daerah penyelesaian 2x +y ≥ 10 berada di atas garis 2x + y = 10.
- Garis 2x + y = 8 melalui titik (8,0) dan (0,4) dan daerah penyelesaian x+2y ≥ 8 berada di atas garis x + 2y = 8.
- Daerah penyelesaian x ≥ 0 berada di kanan sumbu Y.
- Daerah penyelesaian y ≥ 0 berada di atas garis sumbu X.
Daerah penyelesaian terlampir
Titik pojok (4,2), (8,0), dan (0,10) disubstitusikan.
- f(4, 2) = 4c + 8
- f(8, 0) = 8c
- f(0, 10) = 40
Agar (4,2) menjadi titik minimum maka:
4c + 8 ≤ 8c
8 ≤ 4c
2 ≤ c
dan
4c + 8 ≤ 40
4c ≤ 32
c ≤ 8
Sehingga dapat dituliskan:
2 ≤ c ≤ 8 (Pilihan Jawaban D).
· 5.0 (1)
Iklan
Agive S
22 Februari 2023 06:34
<p>waw</p>
waw
· 0.0 (0)
AMBUS A
22 Februari 2023 10:42
kenapa?
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!
Roboguru Plus
Dapatkan pembahasan soal ga pake lama, langsung dari Tutor!


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



