Bu Beni sedang mengatur pola makan untuk kesehatan. Setiap bulan dia membutuhkan paling sedikit 16 unit konsumsi, 18 unit lemak, dan 24 unit protein. Untuk memenuhi kebutuhan tersebut dia membeli dua jenis makanan, yaitu makanan P dan makanan Q. Harga 1 kg makanan P Rp100.000,00 dan harga 1 kg makanan Q Rp50.000,00. Makanan P mengandung 4 unit karbohidrat, 2 unit lemak, dan 12 unit protein, sedangkan makanan Q mengandung 2 unit gula, 6 unit lemak, dan 2 unit protein. Biaya minimum yang harus dikeluarkan Bu Beni setiap bulan butuh kebutuhan, lemak, dan protein terpenuhi adalah.

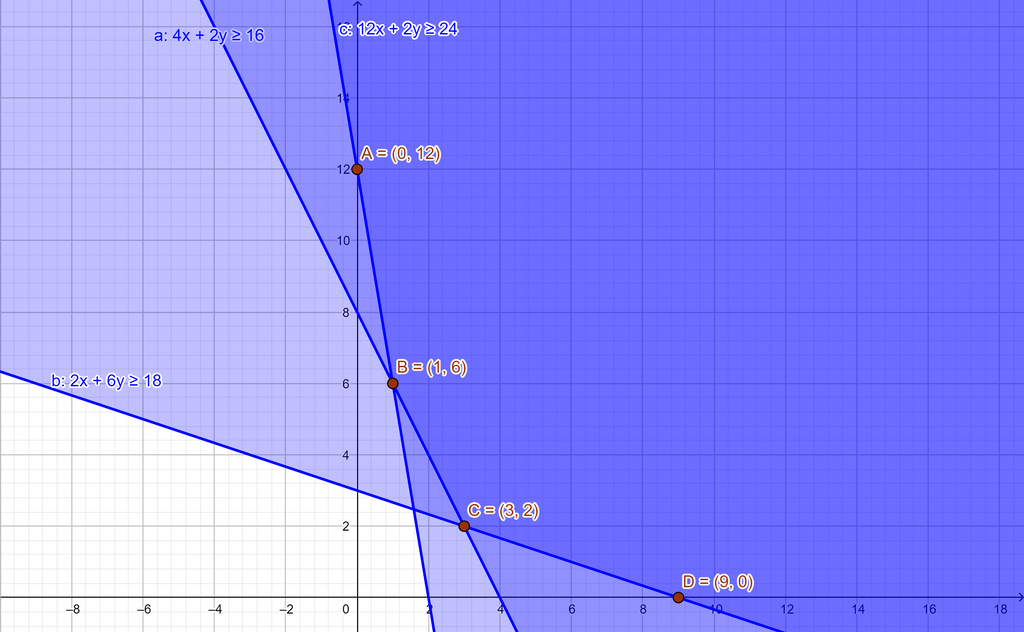
Halo Annisa, kaka bantu jawab yaa:) Jawaban: Rp400.000,00 Konsep: program linier Langkah pengerjaan soal cerita progam linier: 1. Memisalkan dua variabel 2. Buatlah model matematika dan fungsi optimum (fungsi yang akan dimaksimumkan atau diminimumkan) dari soal 3. Cari titik potong setiap pertidaksamaan garis dengan sumbu koordinat 4. Buat gambar dan cari daerah arsirannya 5. Cari semua titik kritis, masukkan ke dalam fungsi optimum 6. Cari nilai maksimum atau minimum Pembahasan: Asumsi koreksian konsumsi = gula = karbohidrat Keperluan paling sedikit 16 unit karbohidrat, 18 lemak dan 24 protein P --> 4 karbohidrat, 2 lemak, 12 protein Q --> 2 karbohidrat, 6 lemak, 2 protein Harga P = Rp100.000,00 Harga Q = Rp50.000,00 Misalkan, jumlah makanan P = p kg dan Q = q kg Dari karbohidrat 4p + 2q ≥ 16 (kemudian kedua ruas dibagi 2) 2p + q ≥ 8 2p + q = 8 p = 0, 2(0) + q = 8 --> q = 8, didapatkan titik (0, 8) q = 0, 2p + 0 = 8 --> p = 4, didapatkan titik (4, 0) Dari lemak 2p + 6q ≥ 18 (kemudian kedua ruas dibagi 2) p + 3q ≥ 9 p + 3q = 9 p = 0, 0 + 3q = 9 --> q = 3, didapatkan titik (0, 3) q = 0, p + 0 = 9 --> p = 9, didapatkan titik (9, 0) Dari protein 12p + 2q ≥ 24 (kemudian kedua ruas dibagi 2) 6p + q ≥ 12 6p + q = 12 p = 0, 6(0) + q = 12 --> q = 12, didapatkan titik (0, 12) q = 0, 6p + 0 = 12 --> p = 2, didapatkan titik (2, 0) Kemudian titik-titik yang didapat diplotkan ke dalam bidang kartesius seperti pada gambar. Didapatkan titik kritis A(0, 12), B(1, 6), C(3, 2) dan D(9, 0) B merupakan perpotongan garis I dan II 6p + q = 12 2p + q = 8 --------------- - 4p = 4 p = 1 --> 2p + q = 8 --> 2(1) + q = 8 --> q = 6 Didapatkan titik B(1, 6) C merupakan perpotongan garis I dan II 2p + q = 8 |×3| 6p + 3q = 24 p + 3q = 9 |×1 | p + 3q = 9 ------------------------------------ - 5p = 15 p = 3 --> p + 3q = 9 --> 3 + 3q = 9 --> 3 = 2 Didapatkan titik C(3, 2) Fungsi optimum diambil dari harga H = harga P + harga Q H = 100.000p + 50.000q Substitusikan titik kritis A(0, 12), B(1, 6), C(3, 2) dan D(9, 0) A(0, 12) H = 100.000p + 50.000q H = 100.000(0) + 50.000(12) H = 0 + 600.000 H = Rp600.000,00 B(1, 6) H = 100.000p + 50.000q H = 100.000(1) + 50.000(6) H = 100.000 + 300.000 H = Rp400.000,00 C(3, 2) H = 100.000p + 50.000q H = 100.000(3) + 50.000(2) H = 300.000 + 100.000 H = Rp400.000,00 D(9, 0) H = 100.000p + 50.000q H = 100.000(9) + 50.000(0) H = 900.000 + 0 H = Rp900.000,00 Pada soal ditanya biaya minimum, cari nilai yang paling kecil biayanya yaitu Rp400.000,00. Jadi, biaya minimumnya adalah Rp400.000,00