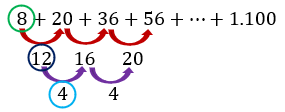Tentukan notasi sigma deret 8 + 20 + 36 + 56 + ... + 1.100 dengan batas atas 30.

Pembahasan

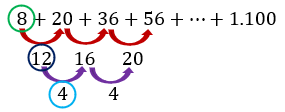
Deret bilangan di atas merupakan deret bilangan bertingkat dua. Rumus suku ke- k untuk barisan bilangan bertingkat dua adalah U k ​ = a + ( k − 1 ) ⋅ b + 2 ( k − 1 ) ( k − 2 ) ​ ⋅ c dengan adalah suku pertama, b adalah selisihsuku pertama dan kedua, dan adalah selisih dari setiap beda. Perhatikan ilustrasi berikut! Dapat diperhatikan bahwa suku pertama deret tersebut adalah a = 8 ,selisihsuku pertama dan kedua adalah b = 12 , danselisih dari setiap beda adalah c = 4 . Oleh karena itu, rumus suku ke- k dari deret tersebut dapat disusun sebagai berikut. U k ​ ​ = = = = = ​ a + ( k − 1 ) ⋅ b + 2 ( k − 1 ) ( k − 2 ) ​ ⋅ c 8 + ( k − 1 ) ⋅ 12 + 2 ( k − 1 ) ( k − 2 ) ​ ⋅ 4 8 + 12 k − 12 + ( k 2 − k − 2 k + 2 ) ⋅ 2 8 + 12 k − 12 + 2 k 2 − 2 k − 4 k + 4 2 k 2 + 6 k ​ Batas bawah sigma adalah , karena 8 merupakan suku pertama deret. Menentukan batas atas sigma: U k ​ = 2 k 2 + 6 k 2 k 2 + 6 k = 1.100 k 2 + 3 k –550 = 0 ( k –22 ) ( k + 25 ) = 0 k = 22 atau k = –25 Untuk k = –25 tidak memenuhi karena k menyatakan letak suku dan harus bilangan asli. Oleh karena itu, diperoleh batas atas k = 22 . Dengan demikian, notasi sigma dari deret tersebut adalah Bentuk notasi sigma dengan batas atas 30: Jadi, notasi sigma deret dengan batas 30 adalah .