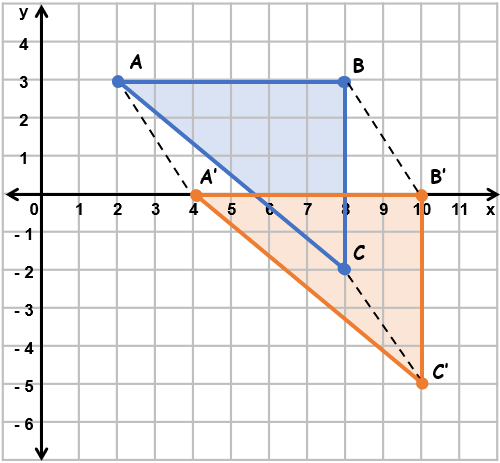
Tentukan bayangan segitiga ABC dengan koordinat titik-titik A ( 2 , 3 ) , B ( 8 , 3 ) , dan C ( 8 , − 2 ) jika ditranslasikan oleh vektor translasi: T ( 2 , − 3 ) . Perhatikan hasil bayangan segitiga yang kalian peroleh: a. Bagaimana bentuk segitiga bayangan tersebut jika dibandingkan dengansegitiga ABC? b. Apakah luas kedua segitiga tersebut sama? Jelaskan dengan perhitungan matematika!

Pembahasan

Misalkan ( x , y ) ditranslasi sebesar ( a , b ) maka bayangan yang dihasilkan adalah ( x ′ , y ′ ) = ( x , y ) + ( a , b ) = ( x + a , y + b ) . a. Akan dicaribayangan dari segitiga ABC, diperoleh perhitungan sebagai berikut A ( 2 , 3 ) ⇒ A ′ ( x ′ , y ′ ) = ( 2 , − 3 ) + ( 2 , 3 ) = ( 2 + 2 , − 3 + 3 ) = ( 4 , 0 ) B ( 8 , 3 ) ⇒ B ′ ( x ′ , y ′ ) = ( 2 , − 3 ) + ( 8 , 3 ) = ( 2 + 8 , − 3 + 3 ) = ( 10 , 0 ) C ( 8 , − 2 ) ⇒ C ′ ( x ′ , y ′ ) = ( 2 , − 3 ) + ( 8 , − 2 ) = ( 2 + 8 , − 3 − 2 ) = ( 10. − 5 ) sehingga diperoleh bayangannya A ′ = ( 4 , 0 ) , B ′ = ( 10 , 0 ) , C ′ = ( 10. − 5 ) . Untuk membandingkan bentuk segitiga ABC dan bayangannya, lebih mudah jika digambarkan pada koordinat kartesius. Dari gambar terlihat bahwa segitiga ABC dan bayangannya memiliki bentuk dan ukuran yang sama persis. Dengan demikian,bentuk segitiga bayangan tersebut jika dibandingkan dengansegitiga ABC adalah sama persis. b. Dari gambar di jawaban (a) terlihat bahwa segitiga ABC dan bayangannya memiliki bentuk dan ukuran yang sama. Hal ini akan kita buktikan dengan perhitungan matematika. Segitiga ABC berbentuk segitiga siku-siku. Sisi tegaknya adalah AB dan BC dengan AB = 6 satuan dan BC = 5 satuan . Luas segitiga ABC diperoleh seperti berikut. L ABC ​ ​ = = = ​ 2 1 ​ × AB × BC 2 1 ​ × 6 × 5 15 satuan luas ​ Bayangan segitiga ABC adalah A ′ B ′ C ′ . Segitiga A ′ B ′ C ′ berbentuk segitiga siku-siku dengan sisi tegaknya A’B’danB’C’ . Panjang A ′ B ′ = 6 satuan dan B ′ C ′ = 5 satuan . Luas segitiga A ′ B ′ C ′ diperoleh seperti berikut. L A ′ B ′ C ′ ​ ​ = = = ​ 2 1 ​ × A ′ B ′ × B ′ C ′ 2 1 ​ × 6 × 5 15 satuan luas ​ Dari perhitungan matematika, terlihat jika luas segitiga ABC dan luas segitiga A ′ B ′ C ′ sama. Dengan demikian dapat disimpulkan jikaluas kedua segitiga tersebut sama terbukti dari perhitungan matematika.