Pertanyaan

Seutas kawat lurus dilengkungkan dan dialiri arus I seperti gambar berikut. Besar induksi magnetik di titik P adalah ....

Seutas kawat lurus dilengkungkan dan dialiri arus I seperti gambar berikut.

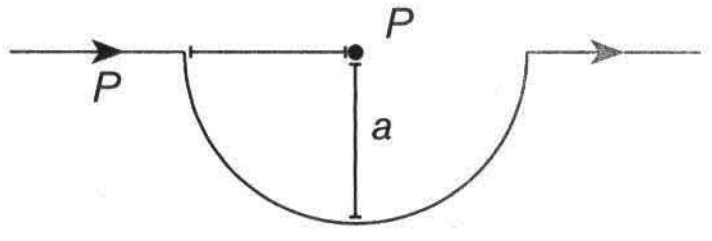
Besar induksi magnetik di titik P adalah .... $\;$

nol
$fraction numerator mu subscript 0 I over denominator pi a end fraction$
$fraction numerator mu subscript 0 I over denominator 2 pi a end fraction$
$fraction numerator mu subscript 0 I over denominator 2 a end fraction$
$fraction numerator mu subscript 0 I over denominator 4 a end fraction$

Y. Maghfirah

Master Teacher

Jawaban terverifikasi

Jawaban

pilihan jawaban yang tepat adalah E

pilihan jawaban yang tepat adalah E space

Pembahasan

Diketahui: Apabila kawat lurus tersebut dianggap panjang, maka yang berpengaruh terhadap induksi magnet pada titik P hanya bagian kawat yang dilengkungkan. Mencari besar induksi magnetik di titik P dengan menggunakan persamaan induksi magnetik pada pusat kawat melingkar: Besar induksi magnetik di titik P adalah Jadi, pilihan jawaban yang tepat adalah E

Diketahui:

r equals a

Apabila kawat lurus tersebut dianggap panjang, maka yang berpengaruh terhadap induksi magnet pada titik P hanya bagian kawat yang dilengkungkan.

Mencari besar induksi magnetik di titik P dengan menggunakan persamaan induksi magnetik pada pusat kawat melingkar:

$B equals fraction numerator mu subscript 0 N I over denominator 2 r end fraction Karena space 1 divided by 2 space lingkaran space maka space N equals 1 half colon B equals fraction numerator mu subscript 0 N I over denominator 2 r end fraction B equals fraction numerator mu subscript 0 I over denominator 2 a end fraction cross times 1 half bold italic B bold equals fraction numerator bold italic mu subscript bold 0 bold italic I over denominator bold 4 bold italic a end fraction$

Besar induksi magnetik di titik P adalah $fraction numerator bold italic mu subscript bold 0 bold italic I over denominator bold 4 bold italic a end fraction$

Jadi, pilihan jawaban yang tepat adalah E space

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.5 (10 rating)

Fauzia Sal Sabila

Bantu banget

Claudyamareshky

Jawaban tidak sesuai Pembahasan tidak lengkap

Pertanyaan serupa

Dua utas kawat dibengkokkan membentuk setengah lingkaran dengan jari-jari a seperti ditunjukkan. Jika setengah lingkaran yang atas memiliki hambatan 2 R Ω dan yang bawah memiliki hambatan R , medan ma...

4.8

Jawaban terverifikasi

Selembar kawat berarus listrik dilengkungan seperti pada gambar. Jika jari - jari kelengkungan sebesar 50 cm, maka besarnya induksi magnetik di pusat kelengkungan adalah ....

4.6

Jawaban terverifikasi

Pada suatu bidang datar terdapat suatu kumparan tipis A dan kawat lurus B, masing - masing dialiri arus sebesar 0,25 A dan 4 A dengan arah seperti gambar. Jari - jari kumparan 4 cm dan jarak pusat kum...

0.0

Jawaban terverifikasi

Perhatikan gambar Suatu penghantar dialiri arus listrik I=9A, jika jari-jari kelengkungan , maka besar induksi magnetik di titik P adalah

120

4.2

Jawaban terverifikasi

Sebuah kawat berarus yang berbentuk seperti gambar di bawah dialiri arus I yang arahnya ditunjukkan oleh panah. Tentukan besar dan arah medan magnet Bi di titik O oleh kawat setengah lingkaran C...

0.0

Jawaban terverifikasi