Pertanyaan

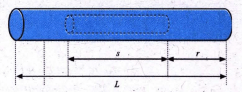
Sebuah silinder dengan jari-jari R 1 dan panjang L terbuat dari bahan kenyal yang homogen. Bahan kenyal tersebut memiliki modulus Young senilai Y . Pada jarak r dari salah satu ujungnya, silinder itu dibuat lubang berbentuk silinder pula dengan panjang s dan jari-jari R 2 . Lubang yang berbentuk silinder itu membujur sedemikian rupa sehingga sumbunya berimpit dengan sumbu silinder besar. Tetapan kenyal silinder tersebut adalah....

Sebuah silinder dengan jari-jari R₁ dan panjang L terbuat dari bahan kenyal yang homogen. Bahan kenyal tersebut memiliki modulus Young senilai Y. Pada jarak r dari salah satu ujungnya, silinder itu dibuat lubang berbentuk silinder pula dengan panjang s dan jari-jari R₂. Lubang yang berbentuk silinder itu membujur sedemikian rupa sehingga sumbunya berimpit dengan sumbu silinder besar. Tetapan kenyal silinder tersebut adalah....

$begin mathsize 14px style fraction numerator Y pi R subscript 1 squared over denominator L space minus space s end fraction space plus space Y pi fraction numerator open parentheses R subscript 1 squared space minus space R subscript 2 squared close parentheses over denominator s end fraction end style$
$begin mathsize 14px style fraction numerator L Y pi space open parentheses R subscript 1 squared space minus space R subscript 2 to the power of 1 close parentheses space plus space s Y pi R subscript 1 squared over denominator s space open parentheses L space minus space s close parentheses end fraction end style$
$begin mathsize 14px style fraction numerator L Y pi space open parentheses R subscript 1 squared space minus space R subscript 2 squared close parentheses space plus space s Y pi R subscript 1 squared over denominator L space open parentheses L space minus space s close parentheses end fraction end style$
$begin mathsize 14px style fraction numerator Y pi squared space R subscript 1 squared space open parentheses R subscript 1 space minus space R subscript 2 close parentheses squared over denominator pi space open parentheses R subscript 1 space minus space R subscript 2 close parentheses squared space open parentheses L space minus space s close parentheses space plus space pi R subscript 1 squared s end fraction end style$
Tidak dapat dihitung

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

N. Puspita

Master Teacher

Jawaban terverifikasi

Pembahasan

Diketahui : l 1 = L-s-r r 1 = R 1 l 2 = s l 3 = r r 3 = R 1 Ditanya : k total ? Penyelesaian : Tetapan kenyal sebuah benda dapat dihitung menggunakan persamaan berikut. Apabila diperhatikan, silinder tersebut terdiri atas 3 bagian yang dirangkai seri. Bagian kiri sebagai benda 1, tengah (yang berlubang) sebagai benda 2, dan bagian kanan sebagai benda 3. Hitung tetapan kenyal masing-masing benda terlebih dahulu. Hitung tetapan kenyal total menggunakan persamaan tetapan kenyal seri. Dengan demikian, tetapan kenyal silinder tersebut adalah . Sepertinya terdapat kesalahan pada pilihan jawaban sehingga tidak ada jawaban yang benar.

Diketahui :

l₁ = L-s-r

r₁ = R₁

l₂ = s

l₃ = r

r₃ = R₁

Ditanya : k_total?

Penyelesaian :

Tetapan kenyal sebuah benda dapat dihitung menggunakan persamaan berikut.

$Y equals fraction numerator k l over denominator A end fraction k equals fraction numerator Y A over denominator l end fraction$

Apabila diperhatikan, silinder tersebut terdiri atas 3 bagian yang dirangkai seri. Bagian kiri sebagai benda 1, tengah (yang berlubang) sebagai benda 2, dan bagian kanan sebagai benda 3. Hitung tetapan kenyal masing-masing benda terlebih dahulu. space

$table attributes columnalign right center left columnspacing 0px end attributes row cell k subscript 1 end cell equals cell fraction numerator Y pi R subscript italic 1 to the power of italic 2 over denominator L italic minus s italic minus r end fraction end cell row cell k subscript 2 end cell equals cell fraction numerator Y pi begin italic style left parenthesis R subscript 1 squared minus R subscript 2 squared right parenthesis end style over denominator s end fraction end cell row cell k subscript 3 end cell equals cell fraction numerator Y pi R subscript italic 1 to the power of italic 2 over denominator r end fraction end cell end table$

Hitung tetapan kenyal total menggunakan persamaan tetapan kenyal seri.

$table attributes columnalign right center left columnspacing 0px end attributes row cell 1 over k subscript t o t a l end subscript end cell equals cell 1 over k subscript 1 plus 1 over k subscript 2 plus 1 over k subscript 3 end cell row cell 1 over k subscript t o t a l end subscript end cell equals cell fraction numerator 1 over denominator fraction numerator Y pi R subscript italic 1 to the power of italic 2 over denominator L italic minus s italic minus r end fraction end fraction plus fraction numerator 1 over denominator fraction numerator Y pi italic left parenthesis R subscript italic 1 to the power of italic 2 italic minus R subscript italic 2 to the power of italic 2 italic right parenthesis over denominator s end fraction end fraction plus fraction numerator 1 over denominator fraction numerator Y pi R subscript italic 1 to the power of italic 2 over denominator r end fraction end fraction end cell row cell 1 over k subscript t o t a l end subscript end cell equals cell fraction numerator L italic minus s italic minus r over denominator Y pi R subscript italic 1 to the power of italic 2 end fraction plus fraction numerator s over denominator Y pi italic left parenthesis R subscript italic 1 to the power of italic 2 italic minus R subscript italic 2 to the power of italic 2 italic right parenthesis end fraction plus fraction numerator r over denominator Y pi R subscript italic 1 to the power of italic 2 end fraction end cell row cell 1 over k subscript t o t a l end subscript end cell equals cell fraction numerator L italic minus s over denominator Y pi R subscript italic 1 to the power of italic 2 end fraction plus fraction numerator s over denominator Y pi italic left parenthesis R subscript italic 1 to the power of italic 2 italic minus R subscript italic 2 to the power of italic 2 italic right parenthesis end fraction end cell row cell 1 over k subscript t o t a l end subscript end cell equals cell fraction numerator L italic minus s italic left parenthesis R subscript italic 1 to the power of italic 2 italic minus R subscript italic 2 to the power of italic 2 italic right parenthesis plus s R subscript italic 1 to the power of italic 2 over denominator Y pi R subscript italic 1 to the power of italic 2 italic left parenthesis R subscript italic 1 to the power of italic 2 italic minus R subscript italic 2 to the power of italic 2 italic right parenthesis end fraction end cell row cell k subscript t o t a l end subscript end cell equals cell fraction numerator Y pi R subscript italic 1 to the power of italic 2 italic left parenthesis R subscript italic 1 to the power of italic 2 italic minus R subscript italic 2 to the power of italic 2 italic right parenthesis over denominator L italic minus s italic left parenthesis R subscript italic 1 to the power of italic 2 italic minus R subscript italic 2 to the power of italic 2 italic right parenthesis plus s R subscript italic 1 to the power of italic 2 end fraction end cell row blank equals cell fraction numerator Y pi squared R subscript italic 1 to the power of italic 2 italic left parenthesis R subscript italic 1 to the power of italic 2 italic minus R subscript italic 2 to the power of italic 2 italic right parenthesis over denominator pi open parentheses L italic minus s close parentheses italic left parenthesis R subscript italic 1 to the power of italic 2 italic minus R subscript italic 2 to the power of italic 2 italic right parenthesis plus pi s R subscript italic 1 to the power of italic 2 end fraction end cell end table$

Dengan demikian, tetapan kenyal silinder tersebut adalah $table attributes columnalign right center left columnspacing 0px end attributes row blank blank cell fraction numerator Y pi squared R subscript italic 1 to the power of italic 2 italic left parenthesis R subscript italic 1 to the power of italic 2 italic minus R subscript italic 2 to the power of italic 2 italic right parenthesis over denominator pi open parentheses L italic minus s close parentheses italic left parenthesis R subscript italic 1 to the power of italic 2 italic minus R subscript italic 2 to the power of italic 2 italic right parenthesis plus pi s R subscript italic 1 to the power of italic 2 end fraction end cell end table$ .

Sepertinya terdapat kesalahan pada pilihan jawaban sehingga tidak ada jawaban yang benar.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

5.0 (1 rating)

xaviera prameswari

Pembahasan lengkap banget Mudah dimengerti Bantu banget Makasih 👍🙏

Pertanyaan serupa

Kalau Anda menekan karet penghapus dengan kuat, bagaimana kondisi karet penghapus tersebut? Jika tekanan Anda lepaskan, bagaimana kondisi karet penghapus tersebut? Jelaskan.

5.0

Jawaban terverifikasi

Sebuah mesin bermassa 400 kg dengan luas penampang 4 × 1 0 − 3 m / s jika modulus elastisnya 2 × 1 0 8 newton dan panjang 2 meter hitung pertambahan panjangnya

0.0

Jawaban terverifikasi

Seutas kawat tembaga memiliki luas 2 mm 2 dan E = 12 × 1 0 11 cm 2 dyne . Kawat tersebut diregangkan oleh gaya 16 × 1 0 6 dyne. Jika panjang tembaga mula-mula 30 cm, pertambahan panjang kawat terseb...

4.3

Jawaban terverifikasi

Panjang tali raket mula-mula30 cm dengan diameter 1,0 mm. Bila tali ditarik dengan gaya 250 N, berapakah pertambahan panjang tali? Diketahui : modulus Young nilon adalah 5 × 1 0 9 N / m 2

5.0

Jawaban terverifikasi

Berikut ini adalah persamaan untuk menentukan modulus young antara perbandingan tengangan dan regangan geser adalah....

5.0

Jawaban terverifikasi