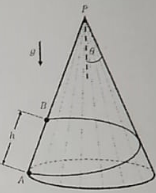
Sebuah gunung dimodelkan sebagai kerucut dengan tinggi H dan sudut setengah bukaanθ, dimana sin θ = 4 1 ​ . Sebuah lintasan yang mengitari gunung dibuat untuk menhubungkan titik A pada dasar gunung dan titik B pada permukaan gunung, dimana puncak gunung (titik P ), titik A , dan titik B terletak pada satu garis lurus. Panjang segmen garis lurus A B adalah h = 15 ​ H ​ . Lintasan dibuat menggunakan kawat dengan panjang minimum yang mengitari gunung. Sebuah partikel yang dapat bergerak bebas tanpagesekan sepanjang lintasan kawat ditembakkan dari titik A dan bergerak menuju titik B . Nyatakan semua jawaban dalam H dan percepatan gravitasi g . Jika partikel ditembakkan dari titik A dengan kalajuan v tersebut, hitung kelajuan partikel di titik B yakni v'.

Sebuah batu yang dilemparkan dengan sudut elevasi 30°, ternyata menumbuk tembok sebuah gedung yang berada 20 3 ​ m di depan tempat pelemparan dan 15 m di atas titik pelemparan. Hitunglah besar dan ara...

Dari titik A dari tanah, sebuah bola dilemparkan dengan kecepatan awal 15 m/s dan sudut elevasi 37° (sin 37°= 0,6) jika g = 10 m/s 2 . Kecepatan bola setelah 0,3 sekon ....

Sebuah bola ditendang dengan sudut elevasi 37° dan kecepatan awal 10 m/s. Kecepatan bola setelah 0,2 detik adalah ... m/ s. ( cos 3 7 ∘ = 5 4 ​ , sin 3 7 ∘ = 5 3 ​ )

Sebuah benda bergerak dengan persamaan r = 3 t 2 − 3 t + 2 dengan r dalam meter dan t dalam sekon. Persamaan kecepatan benda tersebut adalah ....

Benda bergerak dengan kecepatan awal v 0 ​ = ( 2 t + 2 ) m / s , lalu dipercepat dengan percepatan a = ( 3 t − 2 t ) m / s . Persamaan kecepatansaat t sekon adalah ....