Iklan
Pertanyaan
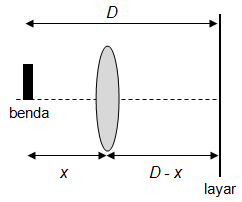
Sebuah benda bercahaya berjarak tetap D dari layar. Kemudian benda tersebut diletakkan di depan sebuah lensa konvergen dengan jarak fokus f sehingga akan membentuk bayangan nyata pada layar untuk dua posisi tertentu, yang satu dengan lainnya berjarak d . Tunjukkan bahwaperbandingan ukuran bayangan pada kedua keadaan ini diberikan oleh ( D + d D − d ) 2 !
Sebuah benda bercahaya berjarak tetap dari layar. Kemudian benda tersebut diletakkan di depan sebuah lensa konvergen dengan jarak fokus sehingga akan membentuk bayangan nyata pada layar untuk dua posisi tertentu, yang satu dengan lainnya berjarak . Tunjukkan bahwa perbandingan ukuran bayangan pada kedua keadaan ini diberikan oleh !
Iklan
YM
Y. Maghfirah
Master Teacher
Jawaban terverifikasi
1
0.0 (0 rating)
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia