Perhatikan gambar berikut! Jika grafik tersebutdicerminkan terhadap sumbu- y , laludigeser sejauh 4 satuan ke kanan dan 1 satuan ke bawah, makapersamaan grafik tersebut setelah adanya perubahan adalah ….

Pembahasan

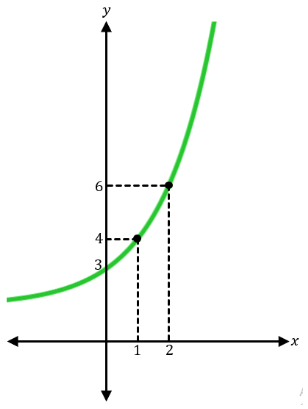
Dari gambar yang diberikan pada soal, dapat diperhatikan bahwa grafik tersebut melalui titik ( 0 , 3 ) , ( 1 , 4 ) , dan ( 2 , 6 ) . Akan disusun persamaan awal grafik tersebut terlebih dahulu. Ingat bahwa bentuk umum dari fungsi eksponen adalah y = a ⋅ b x + c . Substitusikan titik-titik yang dilalui grafik tersebut satu persatu ke dalam y = a ⋅ b x + c untuk mendapatkan tiga persamaan dalam variabel a , b , dan c . Substitusikan titik ( 0 , 3 ) y 3 3 3 a + c ​ = = = = = ​ a ⋅ b x + c a ⋅ b 0 + c a ⋅ 1 + c a + c 3 … ( i ) ​ Substitusikan titik ( 1 , 4 ) y 4 4 ab + c ​ = = = = ​ a ⋅ b x + c a ⋅ b 1 + c ab + c 4 … ( ii ) ​ Substitusikan titik ( 2 , 6 ) y 6 6 a b 2 + c ​ = = = = ​ a ⋅ b x + c a ⋅ b 2 + c a b 2 + c 6 … ( iii ) ​ Selanjutnya, nilai a , b , dan dapat ditentukan dengan metode eliminasi-substitusi. Eliminasi pada persamaan (i) dan (ii) untuk mendapatkan persamaan baru dalam variabel dan b sebagai berikut. a + c = 3 ab + c = 4 a − ab = − 1 ab − a = 1 a ( b − 1 ) = 1 … ( iv ) ​ ​ − ​ Kemudian, eliminasi pada persamaan (ii) dan (iii)untuk mendapatkan persamaan baru dalam variabel dan b sebagai berikut. ab + c = 4 a b 2 + c = 6 ab − a b 2 = − 2 a b 2 − ab = 2 ab ( b − 1 ) = 2 … ( v ) ​ ​ − ​ Perhatikan bahwa persamaan (iv) dan (v) memuat unsur ( b − 1 ) . Karena b merupakan bilangan pokok pada fungsi eksponen y = a ⋅ b x + c , maka nilai b tidak mungkin sama dengan 1 . Akibatnya, nilai dari ( b − 1 ) tidak mungkin sama dengan 0. Oleh karena itu, dapat dilakukan pembagian persamaan (v) oleh persamaan (iv) untuk mendapatkan nilai b sebagai berikut. ab ( b − 1 ) = 2 a ( b − 1 ) = 1 b = 2 ​ ​ ÷ ​ Didapat nilai b adalah 2. Substitusikan nilai b = 2 ke persamaan (iv) untuk mendapatkan nilai sebagai berikut. a ( b − 1 ) a ( 2 − 1 ) a ⋅ 1 a ​ = = = = ​ 1 1 1 1 ​ Didapat nilai adalah 1. Substitusikan nilai a = 1 ke persamaan (i) untuk mendapatkan nilai sebagai berikut. a + c 1 + c 1 + c − 1 c ​ = = = = ​ 3 3 3 − 1 2 ​ Didapat nilai adalah 2 sehingga persamaan awal grafik tersebut dapat disusun sebagai berikut. y y y ​ = = = ​ a ⋅ b x + c 1 ⋅ 2 x + 2 2 x + 2 ​ Dengan demikian, persamaan awal grafik tersebut adalah y = 2 x + 2. Pada soal, diketahui bahwa grafik tersebutdicerminkan terhadap sumbu- y , laludigeser sejauh 4 satuan ke kanan dan 1 satuan ke bawah. Ingat beberapa konsep perubahan grafik berikut! Jika grafik y = f ( x ) dicerminkan terhadap sumbu- y , maka bayangannya adalah y = f ( − x ) . Jika grafik y = f ( x ) digeser sejauh satuan ke kanan, maka bayangannya adalah y = f ( x − p ) . Jika grafik y = f ( x ) digeser sejauh q satuan ke bawah, maka bayangannya adalah y = f ( x ) − q . Berdasarkan konsep tersebut, hasil bayangan grafik y = f ( x ) jika dicerminkan terhadapsumbu- y , lalu digeser sejauh satuan ke kanan dan q satuan ke bawah adalah y = f ( − ( x − p ) ) − q . Oleh karena itu, hasil bayangan grafik y = 2 x + 2 jikadicerminkan terhadap sumbu- y , laludigeser sejauh 4 satuan ke kanan dan 1 satuan ke bawah adalah sebagai berikut. y = 2 x + 2 y = ( 2 − ( x − 4 ) + 2 ) − 1 y = 2 − x + 4 + 2 − 1 y = 2 − x + 4 + 1 y = 2 4 − x + 1 Dengan demikian,persamaan grafik tersebut setelah adanya perubahan adalah y = 2 4 − x + 1. Jadi, jawaban yang tepat adalah C.