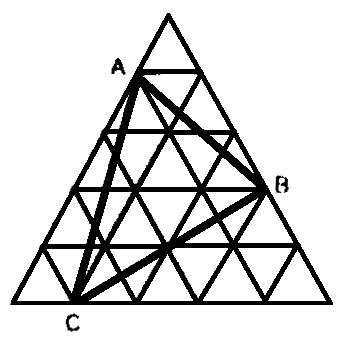
Diketahui:
- 1 segitga sama sisi besar = 25 segitiga sama sisi kecil
- luas segitiga sama sisi kecil,

Ditanya: luas segitiga  ,
, 
Jawab:
Jika gambar di atas, digambarkan kembali seperti berikut:
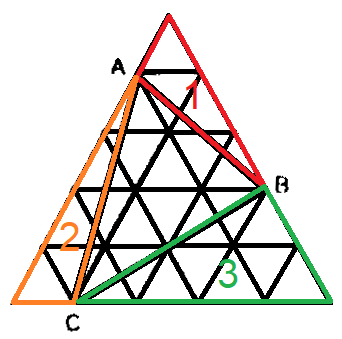
Dapat terlihat pada gambar, jika segitiga sama sisi besar dibangun oleh segitiga  , segitiga 1, segitiga 2, dan segitiga 3. Dengan demikian, luas segitiga
, segitiga 1, segitiga 2, dan segitiga 3. Dengan demikian, luas segitiga  dapat dicari dengan mengurangkan luas segitiga sama sisi besar dengan luas tiga segitiga sisanya, yang dirumuskan sebagai berikut:
dapat dicari dengan mengurangkan luas segitiga sama sisi besar dengan luas tiga segitiga sisanya, yang dirumuskan sebagai berikut:

Oleh karena luas segitiga sama sisi besar  dan luas tiga segitiga
dan luas tiga segitiga  ,
,  ,
,  belum diketahui, maka akan dicari tahu terlebih dahulu.
belum diketahui, maka akan dicari tahu terlebih dahulu.
Mencari luas segitiga sama sisi besar 
Oleh karena segitiga sama sisi besar dibentuk dari 25 segitiga sama sisi kecil dan luas segitiga sama sisi kecil  , maka luas segitiga sama sisi besar adalah
, maka luas segitiga sama sisi besar adalah

Mencari luas tiga segitiga  ,
,  ,
, 
Oleh karena panjang alas dan tinggi dari ketiga segitiga tersebut tidak diketahui, maka dengan memisalkan panjang sisi segitiga kecil  dan mengetahui bahwa setiap sudut dari segitiga sama sisi adalah
dan mengetahui bahwa setiap sudut dari segitiga sama sisi adalah  ,
,

diperoleh bahwa, pada masing-masing segitiga, terdapat dua sisi yang dapat dicari dan mengapit satu sudut yang nilainya diketahui. Dengan demikian, luas segitiga dapat dicari dengan menggunakan aturan sinus.
Rumus luas segitiga  dengan aturan sinus adalah
dengan aturan sinus adalah

dengan  dan
dan  adalah dua panjang sisi segitiga yang mengapit sudut
adalah dua panjang sisi segitiga yang mengapit sudut  .
.
Oleh karena itu, diperoleh:
- Pada segitiga 1, sisi yang mengapit sudut
 adalah
adalah  dan
dan  sehingga dengan menyubtitusi pada rumus luas segitiga menggunakan aturan sinus di atas, diperoleh
sehingga dengan menyubtitusi pada rumus luas segitiga menggunakan aturan sinus di atas, diperoleh

- Pada segitiga 2, sisi yang mengapit sudut
 adalah
adalah  dan
dan  sehingga dengan menyubtitusi pada rumus luas segitiga menggunakan aturan sinus di atas, diperoleh
sehingga dengan menyubtitusi pada rumus luas segitiga menggunakan aturan sinus di atas, diperoleh

- Pada segitiga 3, sisi yang mengapit sudut
 adalah
adalah  dan
dan  sehingga dengan menyubtitusi pada rumus luas segitiga menggunakan aturan sinus di atas, diperoleh
sehingga dengan menyubtitusi pada rumus luas segitiga menggunakan aturan sinus di atas, diperoleh

Kemudian, dengan menyubtitusi  ,
,  ,
,  , dan
, dan  yang telah didapatkan ke rumus mencari luas
yang telah didapatkan ke rumus mencari luas  , diperoleh
, diperoleh

dan dengan mengetahui rumus luas segitiga sama sisi dengan panjang sisi  , yaitu
, yaitu  , maka karena luas segitiga sama sisi kecil
, maka karena luas segitiga sama sisi kecil  dan panjang sisi dimisalkan
dan panjang sisi dimisalkan  , diperoleh
, diperoleh

sehingga dengan menyubtitusi nilai  ke persamaan
ke persamaan  yang masih terdapat variable
yang masih terdapat variable  di atas, diperoleh
di atas, diperoleh

Jadi, luas segitiga  adalah
adalah  .
.