Pertanyaan

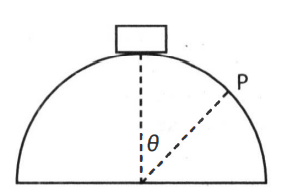
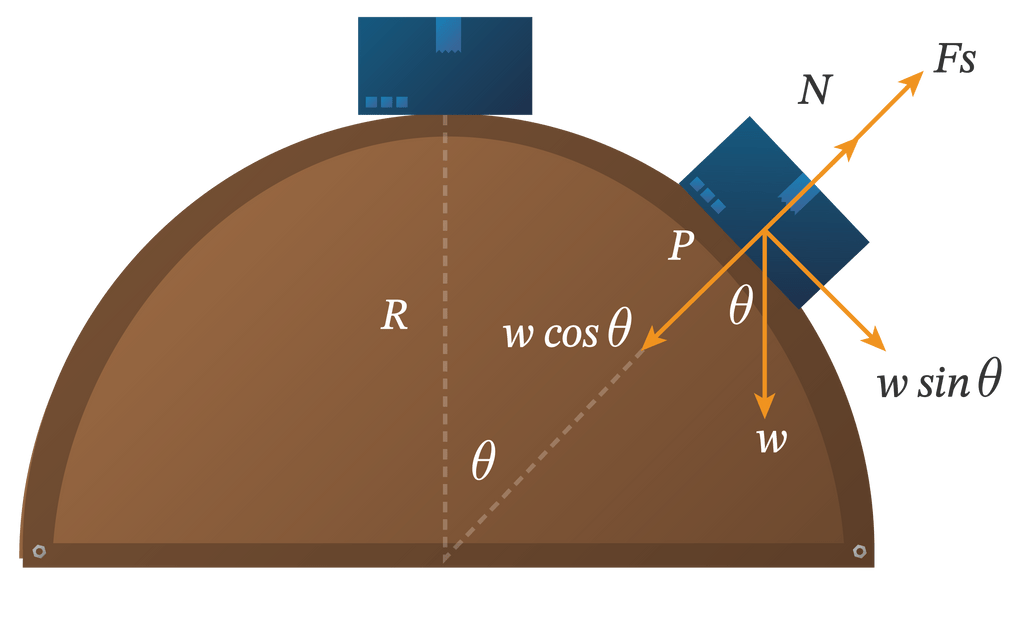
Pada gambar di atas, sebuah balok dengan massa 4 kg berada di puncak bidang setengah bola berjari-jari 30 cm. Permukaan bidang sangat licin sehingga gangguan kecil membuat benda meluncur dan meninggalkan bidang di titlk P (setelah bergerak sejauh θ putaran). Jika percepatan gravitasi bumi, g = 10 m/s 2 , energi kinetik bola ketika meninggalkan bidang (di titik P) adalah .... (SIMAK UI)

Pada gambar di atas, sebuah balok dengan massa 4 kg berada di puncak bidang setengah bola berjari-jari 30 cm. Permukaan bidang sangat licin sehingga gangguan kecil membuat benda meluncur dan meninggalkan bidang di titlk P (setelah bergerak sejauh $θ$ putaran). Jika percepatan gravitasi bumi, g = 10 m/s² , energi kinetik bola ketika meninggalkan bidang (di titik P) adalah ....

(SIMAK UI) $\;$

20 joule $\;$
16 joule $\;$
8 joule $\;$
4 joule $\;$
2 joule $\;$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

Y. Maghfirah

Master Teacher

Jawaban terverifikasi

Jawaban

jawabannya adalah D.

jawabannya adalah D. $\;$

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah D. Diketahui : m = 4kg R = 30 cm = 0,3 m g =10 m/s 2 Ditanyakan : Ek saat bola meninggalkan bidang ... ? Penyelesaian : Perhatikan gambar berikut Untuk mencari energi kinetik kita dapat menggunakan Hukum I Newton dan Hukum kekekalan energi mekanik sebagai berikut Mencari Nilai kecepatan ∑ F F s + N R m v 2 + 0 v 2 = = = = 0 W cos θ m g cos θ g R cos θ .... ( 1 ) Tepat saat balok meninggalkan titik P, gaya normal ( N ) bernilai nol. Hukum kekekalan energi mekanik di titik puncak dan titik P E m 1 E p 1 + E k 1 m g R + 0 g r v 2 v 2 = = = = = = E m p E p p + E k p m g h p + 2 1 m v 2 g r c os θ + 2 1 v 2 2 g R − 2 g R cos θ 2 g R ( 1 − cos θ ) .... ( 2 ) Maka akan didapat nilai cos θ dengan menyamakan persamaan (1) dan (2) g R cos θ cos θ 2 1 cos θ cos θ = = = = 2 g R ( 1 − cos θ ) 2 ( 1 − cos θ ) 1 − cos θ 3 2 Energi kinetik Jadi energi kinetik balok di titik P adalah E k p = = = = 2 1 m v 2 2 1 m g R cos θ 2 1 ⋅ 4 ⋅ 10 ⋅ 0 , 3 ⋅ 3 2 4 J Oleh karena itu, jawabannya adalah D.

Jawaban yang benar untuk pertanyaan tersebut adalah D.

Diketahui :

m = 4kg
R = 30 cm = 0,3 m
g =10 m/s²

Ditanyakan : Ek saat bola meninggalkan bidang ... ?

Penyelesaian :

Perhatikan gambar berikut

Untuk mencari energi kinetik kita dapat menggunakan Hukum I Newton dan Hukum kekekalan energi mekanik sebagai berikut

Mencari Nilai kecepatan

$\sum F F_{s} + N \frac{m v ^{2}}{R} + 0 v^{2} = = = = 0 W cos θ m g cos θ g R cos θ .... (1)$

Tepat saat balok meninggalkan titik P, gaya normal (N) bernilai nol.

Hukum kekekalan energi mekanik di titik puncak dan titik P

$E m_{1} E p_{1} + E k_{1} m g R + 0 g r v^{2} v^{2} = = = = = = E m_{p} E p_{p} + E k_{p} m g h_{p} + \frac{1}{2} m v^{2} g r c os θ + \frac{1}{2} v^{2} 2 g R - 2 g R cos θ 2 g R (1 - cos θ) .... (2)$

Maka akan didapat nilai cos $θ$ dengan menyamakan persamaan (1) dan (2)

$g R cos θ cos θ \frac{1}{2} cos θ cos θ = = = = 2 g R (1 - cos θ) 2 (1 - cos θ) 1 - cos θ \frac{2}{3}$

Energi kinetik

Jadi energi kinetik balok di titik P adalah

$E k_{p} = = = = \frac{1}{2} m v^{2} \frac{1}{2} m g R cos θ \frac{1}{2} \cdot 4 \cdot 10 \cdot 0, 3 \cdot \frac{2}{3} 4 J$

Oleh karena itu, jawabannya adalah D. $\;$

Buka akses jawaban yang telah terverifikasi

Yah, akses pembahasan gratismu habis

atau

Dapatkan jawaban pertanyaanmu di AiRIS. Langsung dijawab oleh bestie pintar

Tanya Sekarang

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

0.0 (0 rating)

Pertanyaan serupa

Soal terdiri atas 3 bagian, yaitu PERNYATAAN; kata SEBAB; dan ALASAN yang disusun berurutan. Sebuah kubus yang meluncur turun tanpa gesekan pada sebuah bidang miring akan mengalami percepatan tetap...

0.0

Jawaban terverifikasi

Sebuah balok dengan berat W newton terletak pada sebuah bidang datar. Pada saat t = 0 s balok diam. Kemudian, dari waktu t = 0 s sampai t = 5 s balok didorong dengan gaya konstan F newton sejajar bida...

0.0

Jawaban terverifikasi

Suatu balok bermassa 2 kg yang berada pada suatu bidang datar licin mengalami gaya konstan F = 10 newton dengan arah seperti ditunjukkan gambar. Kecepatan balok pada saat t = 0 sekon adalah 2 m/s kear...

3.6

Jawaban terverifikasi

N buah balok dengan massa yang sama di ataslantai yang licin disusun seperti pada gambar. Balok yang paling kanan ditarik dengan gaya F kekanan. Besarnya tegangan tali antara balok 2 dan3 adalah...

3.0

Jawaban terverifikasi

Mobil 700 kg mogok di jalan yang mendatar. Kabel horizontal mobil derek yang dipakai untuk menyeretnya akan putus jika tegangan di dalamnya melebihi 1.400 N. Percepatan maksimum yang dapat diterima mo...

4.4

Jawaban terverifikasi

Tanya ke AiRIS

Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

Chat AiRIS