Himpunan penyelesaian dari pertidaksamaan adalah ....

Pembahasan

Dengan definisi nilai mutlak, diperoleh tiga hasil sebagai berikut. dan serta Gabungan daerah untuk interval nilai di atas menghasilkan 4 daerah sebagai berikut ini. Akan dibagi menjadi beberapa kasus per daerah, yaitu , , , dan . Kasus I Untuk interval , diperoleh perhitungan sebagai berikut. Kemudian, dengan menggunakan definisi nilai mutlak kita dapatkan hasil sebagai berikut. Dengan kata lain, kasus ini terbagi lagi menjadi dua bagian, yaitu dan dengan memperhatikan juga bahwa harus terpenuhi. Jika , maka sehingga didapat perhitungan sebagai berikut. Karena memenuhi , maka merupakan penyelesaian. Kemudian, jika ,maka sehingga didapat perhitungan sebagai berikut. Karena dari perhitungan ini menghasilkan pernyataan yang bernilai SALAH, maka dari sini tidak dapat ditarik kesimpulan apapun. Dengan demikian, kesimpulan yang didapat adalah . Jika diiris dengan , maka didapat himpunan penyelesaian dari Kasus I adalah . Untuk lebih jelasnya, perhatikan garis bilangan berikut! 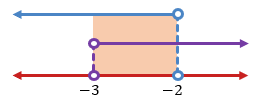Kasus II Untuk interval , diperoleh perhitungan sebagai berikut. Perhatikan bahwa untuk berapun nilai , pertidaksamaan akan bernilai benar. Sehingga himpunan penyelesaian pertidaksamaan tersebut adalah seluruh nilai bilangan real. Dengan kata lain, kesimpulan yang didapat dari Kasus II adalah irisan himpunan penyelesaian dan , yaitu .Untuk lebih jelasnya, perhatikan garis bilangan berikut! Kasus III Untuk interval , diperoleh perhitungan sebagai berikut. Kemudian, dengan menggunakan definisi nilai mutlak kita dapatkan hasil sebagai berikut. Dengan kata lain, kasus ini terbagi lagi menjadi dua bagian, yaitu dan dengan memperhatikan juga bahwa harus terpenuhi. Jika , maka sehingga didapat perhitungan sebagai berikut. Karena memenuhi , maka merupakan penyelesaian. Kemudian, jika , maka sehingga didapat perhitungan sebagai berikut. Karena memenuhi , maka juga merupakan penyelesaian. Penyelesaian dari Kasus III adalahirisan dari interval , , dan pada garis bilangan berikut ini. 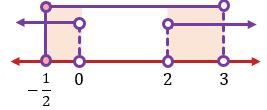Dengan demikian, daerah himpunan penyelesian untuk Kasus III adalah . KasusIV Untuk interval ,diperoleh perhitungan sebagai berikut. Perhatikan bahwa untuk berapun nilai , pertidaksamaan akan bernilai benar sehingga himpunan penyelesaian dari Kasus IV adalah irisan dari dan ,yaitu . Untuk lebih jelasnya, perhatikan garis bilangan berikut! Jika kita gabungkan daerah himpunan penyelesaian dari kempat daerah di atas, yaitu , , dan ke dalam sebuah garis bilangan, akan diperoleh garis bilanganberikut ini. 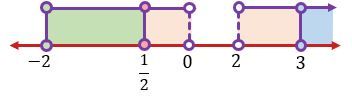Diperoleh himpunan penyelesaian dari pertidaksamaan adalah . Jadi, jawaban yang tepat adalah E.