Untuk menggambarkan sketsa grafik fungsi kuadrat  , ada 4 aspek yang perlu diperhatikan:
, ada 4 aspek yang perlu diperhatikan:
- Nilai
 ; jika
; jika  maka parabola terbuka ke atas, dan jika
maka parabola terbuka ke atas, dan jika  maka parabola terbuka ke bawah.
maka parabola terbuka ke bawah.
- Nilai
 ; jika
; jika  maka parabola memotong sumbu-
maka parabola memotong sumbu- di dua titik. Jika
di dua titik. Jika  maka parabola memotong sumbu-
maka parabola memotong sumbu- , dan jika
, dan jika  maka parabola tidak memotong dan tidak menyinggung sumbu-
maka parabola tidak memotong dan tidak menyinggung sumbu- .
.
- Nilai
 ;
;  adalah koordinat titik potong parabola dengan sumbu-
adalah koordinat titik potong parabola dengan sumbu- .
.
- Koordinat titik ekstrim
 , dengan
, dengan  dan
dan  .
.
Perhatikan bahwa fungsi kuadrat  mempunyai nilai
mempunyai nilai  ,
,  , dan
, dan  .
.
Karena  , maka parabola
, maka parabola  terbuka ke atas.
terbuka ke atas.
Selanjutnya, nilai diskriminannya adalah

Karena nilai  , maka parabola
, maka parabola  memotong sumbu-
memotong sumbu- di dua titik. Koordinat titik-titik potongnya dengan sumbu-
di dua titik. Koordinat titik-titik potongnya dengan sumbu- ditentukan dengan mensubstitusikan nilai
ditentukan dengan mensubstitusikan nilai  ke fungsi kuadrat.
ke fungsi kuadrat.
Perhatikan bahwa

dan mengakibatkan

sehingga koordinat titik-titik potong parabola dengan sumbu- adalah
adalah  dan
dan  .
.
Berikutnya, karena  maka koordinat titik potong parabola dengan sumbu-
maka koordinat titik potong parabola dengan sumbu- adalah
adalah  .
.
Terakhir, kita akan menghitung koordinat titik puncak parabola  .
.

dan

Jadi, koordinat titik puncak grafik fungsi kuadrat  adalah
adalah  .
.
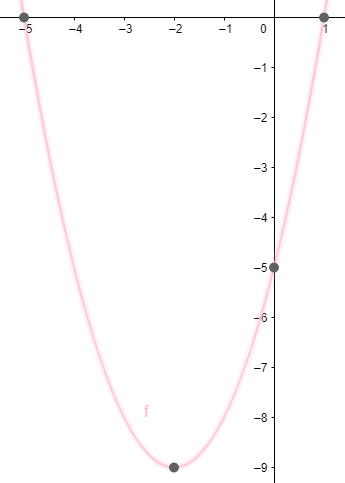
Dengan demikian, sketsa grafik fungsi kuadrat  adalah
adalah
Selanjutnya, ada 3 langkah untuk menentukan fungsi invers, yaitu:
1. Ubahlah bentuk  menjadi bentuk
menjadi bentuk  .
.
2. Tuliskan  sebagai
sebagai  sehingga
sehingga  .
.
3. Ubahlah variabel y dengan x sehingga diperoleh rumus fungsi invers  .
.
Oleh karena itu, misalkan  . Maka
. Maka

Karena bentuk akar selalu bernilai nonnegatif, maka

Dengan demikian,  dan mengakibatkan
dan mengakibatkan  .
.
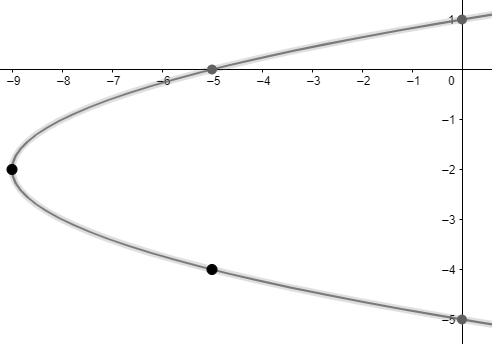
Untuk menggambarkan grafik  , kita akan menentukan beberapa pasangan titik yang dilalui oleh grafik tersebut.
, kita akan menentukan beberapa pasangan titik yang dilalui oleh grafik tersebut.
Untuk  , maka
, maka

Untuk  , maka
, maka

sehingga

Untuk  , maka
, maka

sehingga

Dengan menggambarkan titik-titik tersebut pada bidang Kartesius, diperoleh grafik sebagai berikut: