Pertanyaan

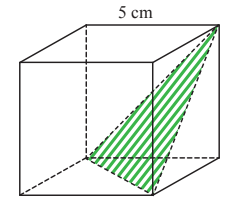
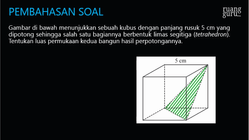
Gambar di bawah menunjukkan sebuah kubus dengan panjang rusuk 5 cm yang dipotong sehingga salah satu bagiannya berbentuk limas segitiga ( tetrahedron ). Tentukan luas permukaan kedua bangun hasil perpotongannya.

Gambar di bawah menunjukkan sebuah kubus dengan panjang rusuk $5 cm$ yang dipotong sehingga salah satu bagiannya berbentuk limas segitiga (tetrahedron). Tentukan luas permukaan kedua bangun hasil perpotongannya.

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

F. Ayudhita

Master Teacher

Jawaban terverifikasi

Jawaban

luas permukaan bangun I dan luas permukaan bangun II .

luas permukaan bangun I

dan luas permukaan bangun II

Pembahasan

Kita misalkan: Bangun I: Limas segitiga hasil perpotongan Bangun II: Kubus setelah dipotong limas (Bangun I) a. Luas Permukaan (LP) Bangun I Bangun I berbentuk limas, yang terdiri dari: - segitiga yang diarsir - 3 segitiga siku-siku (1/2 dari sisi kubus) Sehingga kita dapat menentukan luas permukaannya (LP) sebagai berikut: 1) Luas segitiga arsir dimana dan sehingga kita dapat luas segitiga yang diarsir sebagai berikut: 2) Luas segitiga siku-siku: Sehingga Luas Permukaan (LP) BangunI: b. Luas Permukaan (LP) Bangun II Bangun II berbentuk kubus yang terpotong oleh limas (Bangun I), sehingga kita bisa tuliskan sebagai berikut: Jadi, luas permukaan bangun I dan luas permukaan bangun II .

Kita misalkan:

Bangun I: Limas segitiga hasil perpotongan
Bangun II: Kubus setelah dipotong limas (Bangun I)

a. Luas Permukaan (LP) Bangun I

Bangun I berbentuk limas, yang terdiri dari:

- segitiga yang diarsir
- 3 segitiga siku-siku (1/2 dari sisi kubus)

Sehingga kita dapat menentukan luas permukaannya (LP) sebagai berikut:

1) Luas segitiga arsir $begin mathsize 14px style equals fraction numerator a cross times t over denominator 2 end fraction end style$
dimana

dan
begin mathsize 14px style t squared equals open parentheses 5 square root of 2 close parentheses squared minus open parentheses 1 half 5 square root of 2 close parentheses squared t squared equals 50 minus 12 comma 5 t squared equals 37 comma 5 t equals square root of 37 comma 5 end root end style

sehingga kita dapat luas segitiga yang diarsir sebagai berikut:

$begin mathsize 14px style table attributes columnalign right center left columnspacing 0px end attributes row cell luas space segitiga space arsir end cell equals cell fraction numerator a cross times t over denominator 2 end fraction end cell row blank equals cell fraction numerator 5 square root of 2 cross times square root of 37 comma 5 end root over denominator 2 end fraction end cell row blank equals cell fraction numerator 5 square root of 75 over denominator 2 end fraction end cell row blank equals cell fraction numerator 25 square root of 3 over denominator 2 end fraction end cell row blank equals cell 12 comma 5 square root of 3 end cell end table end style$

2) Luas segitiga siku-siku:

$begin mathsize 14px style table attributes columnalign right center left columnspacing 0px end attributes row cell Luas space segitiga space siku minus siku end cell equals cell fraction numerator a cross times t over denominator 2 end fraction end cell row blank equals cell fraction numerator 5 cross times 5 over denominator 2 end fraction end cell row blank equals cell 12 comma 5 end cell end table end style$

Sehingga Luas Permukaan (LP) Bangun I:

b. Luas Permukaan (LP) Bangun II

Bangun II berbentuk kubus yang terpotong oleh limas (Bangun I), sehingga kita bisa tuliskan sebagai berikut:

Error converting from MathML to accessible text.

Jadi, luas permukaan bangun I dan luas permukaan bangun II .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

3.8 (5 rating)

....

suara nya kecil bgtt maszeeehh

pristiani

Jawaban tidak sesuai

Pertanyaan serupa

Limas dengan alas persegi dengan sisi 12 cm , tinggi limas 8 cm . Tentukan a. Luas

2.7

Jawaban terverifikasi

Perhatikan bangun limas TABCD dengan panjang alas limas persegi = 10 cm dan tinggi limas 24 cm ! Hitunglah luas limas TABCD dengan rumus 2 1 K a t s + L a !

0.0

Jawaban terverifikasi

Perhatikan bangun limas TABCD dengan panjang alas limas persegi = 10 cm dan tinggi limas 24 cm ! Berapa jumlah luas bangun ABCD, ABT, BCT, ADT, dan CDT?

0.0

Jawaban terverifikasi

Diketahui keliling alas sebuah limas yang berbentuk persegi adalah 64 cm. Tinggi limas 15 cm. Luas seluruh permukaan limas adalah ...

5.0

Jawaban terverifikasi

Perhatikan gambar limas O.KLMN berikut. Alas limas merupakan persegi yang memiliki panjang sisi 13 cm .Jika sisi tegak limas merupakan segitiga sama kaki dengan tinggi 18 cm ,tentukan. a. luas ...

4.9

Jawaban terverifikasi