Pertanyaan

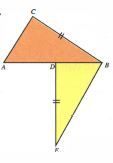
Dua buah segitiga, yaitu △ ABC dan △ BDE kongruen dengan AB = BE . Tentukan: a. besar ∠ ABC , jika ∠ CAD = ∠ DBE = 6 0 ∘ dan ∠ BED = 5 0 ∘ . b. luas △ BDE , jika ∠ CAD = 6 0 ∘ , ∠ ACB = 9 0 ∘ , dan AC = 10 cm !

Dua buah segitiga, yaitu $△ ABC$ dan $△ BDE$ kongruen dengan $AB = BE$ .

Tentukan:

a. besar $∠ ABC$ , jika $∠ CAD = ∠ DBE = 6 0^{\circ}$ dan $∠ BED = 5 0^{\circ}$ .

b. luas $△ BDE$ , jika $∠ CAD = 6 0^{\circ}$ , $∠ ACB = 9 0^{\circ}$ , dan $AC = 10 cm$ !

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

E. Lestari

Master Teacher

Mahasiswa/Alumni Universitas Sebelas Maret

Jawaban terverifikasi

Jawaban

luas △ BDE = 5 3 cm 2 .

luas

△ BDE = 53 cm^{2}

Pembahasan

Jawaban yang benar untuk untuk pertanyaan a dan b adalah dan luas △ BDE = 5 3 cm 2 . Dua Segitiga yang Kongruen Dua segitiga dikatakan kongruen jika dan hanya jika memenuhi syarat berikut: sisi-sisi yang bersesuaian sama panjang. sudut yang bersesuaian sama besar. a.besar ∠ ABC , jika ∠ CAD = ∠ DBE = 6 0 ∘ dan ∠ BED = 5 0 ∘ . Mari kita asumsikan △ ABC dan △ BDE adalah segitiga siku-siku. Dengan siku-siku △ ABC berada di C dan siku-siku △ BDE berada di D . Sehingga besar ∠ ACB = ∠ BDE = 9 0 ∘ . Ingat besar sudut dalam segitiga adalah 18 0 ∘ . Sudut yang bersesuaian dalam segitiga tersebut adalah: ∠ ACB ∠ CAB ∠ ABC = = = = = = ∠ BDE = 9 0 ∘ ∠ DBE = 6 0 ∘ ∠ BED = ... ? 18 0 ∘ − ( 9 0 ∘ + 6 0 ∘ ) 18 0 ∘ − 15 0 ∘ 3 0 ∘ Sudut yang bersesuaian dengan ∠ ABC adalah ∠ BED , karena diapit oleh dua sisi yang sama panjang. Besar ∠ ABC = ∠ BED = 3 0 ∘ . Bukan 5 0 ∘ seperti yang diketahui dalam soal. Dengan demikian, besar ∠ ABC = ∠ BED = 3 0 ∘ . b. Luas △ BDE . Dengan menggunakan sifat dua segitiga yang kongruen, maka diperoleh bahwa: BD = AC = 10 cm Untuk mencari tinggi dari segitiga BDE akan digunakan maka kita gunakan perbandingan sisi dalam segitiga siku-siku istimewa yaitu 9 0 ∘ : 6 0 ∘ : 3 0 ∘ = 2 : 3 : 1 . Sehingga diperoleh: BD AC 10 10 10 ED ED = = = = ED BC ED 3 10 3 3 Luas △ BDE L = = = = 2 1 × a × t 2 1 × BD × ED 2 1 × 10 × 3 5 3 Dengan demikian, luas △ BDE = 5 3 cm 2 .

Jawaban yang benar untuk untuk pertanyaan a dan b adalah $\boldsymbol\angle\mathbf{ABC}\boldsymbol=\boldsymbol\angle\mathbf{BED}\boldsymbol=\mathbf{30}\boldsymbol\textdegree$ dan luas $△ BDE = 53 cm^{2}$ .

Dua Segitiga yang Kongruen

Dua segitiga dikatakan kongruen jika dan hanya jika memenuhi syarat berikut:

sisi-sisi yang bersesuaian sama panjang.
sudut yang bersesuaian sama besar.

a. besar $∠ ABC$ , jika $∠ CAD = ∠ DBE = 6 0^{\circ}$ dan $∠ BED = 5 0^{\circ}$ .

Mari kita asumsikan $△ ABC$ dan $△ BDE$ adalah segitiga siku-siku. Dengan siku-siku $△ ABC$ berada di $C$ dan siku-siku $△ BDE$ berada di $D$ . Sehingga besar $∠ ACB = ∠ BDE = 9 0^{\circ}$ .

Ingat besar sudut dalam segitiga adalah $18 0^{\circ}$ .

Sudut yang bersesuaian dalam segitiga tersebut adalah:

$∠ ACB ∠ CAB ∠ ABC = = = = = = ∠ BDE = 9 0^{\circ} ∠ DBE = 6 0^{\circ} ∠ BED = ... ? 18 0^{\circ} - (9 0^{\circ} + 6 0^{\circ}) 18 0^{\circ} - 15 0^{\circ} 3 0^{\circ}$

Sudut yang bersesuaian dengan $∠ ABC$ adalah $∠ BED$ , karena diapit oleh dua sisi yang sama panjang. Besar $∠ ABC = ∠ BED = 3 0^{\circ}$ . Bukan $5 0^{\circ}$ seperti yang diketahui dalam soal.

Dengan demikian, besar $∠ ABC = ∠ BED = 3 0^{\circ}$ .

b. Luas $△ BDE$ .

Dengan menggunakan sifat dua segitiga yang kongruen, maka diperoleh bahwa:

$BD = AC = 10 cm$

Untuk mencari tinggi dari segitiga $BDE$ akan digunakan maka kita gunakan perbandingan sisi dalam segitiga siku-siku istimewa yaitu $9 0^{\circ} : 6 0^{\circ} : 3 0^{\circ} = 2 : 3 : 1$ . Sehingga diperoleh:

$\frac{AC}{BD} \frac{10}{10} 10 ED ED = = = = \frac{BC}{ED} \frac{3}{ED} 1033$

Luas $△ BDE$

$L = = = = \frac{1}{2} \times a \times t \frac{1}{2} \times BD \times ED \frac{1}{2} \times 10 \times 3 53$

Dengan demikian, luas $△ BDE = 53 cm^{2}$ .

Buka akses jawaban yang telah terverifikasi

Yah, akses pembahasan gratismu habis

atau

Dapatkan jawaban pertanyaanmu di AiRIS. Langsung dijawab oleh bestie pintar

Tanya Sekarang

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

5.0 (2 rating)

Shabiyya K. Azkatrystan

Pembahasan lengkap banget Mudah dimengerti Bantu banget Makasih ❤️

Pertanyaan serupa

Perhatikan gambar berikut. Dari titik Bditarik garis sejajar ACke bawah dan dari titik A ditarik garis sejajar BCsehingga memotong garis sebelumnya di D. △ ABC ≅ △ BAD menurut aksioma ....

4.7

Jawaban terverifikasi

Diketahui segitiga PQR dansegitiga KLM kongruen. Jika sudut P = 5 0 ∘ , sudut Q = 6 0 ∘ , sudut K = 6 0 ∘ dan sudut L = 7 0 ∘ , pasangan sisi yang sama panjang adalah ....

3.9

Jawaban terverifikasi

Diketahui panjang BC = CD . △ CDA ≅ △ CBE menurut aksioma ....

4.8

Jawaban terverifikasi

Perhatikan gambar di bawah ini. DIketahui ∠1 = ∠2 = ∠3 . ES = DT . Dua segitiga yang kongruen adalah ….

4.2

Jawaban terverifikasi

Perhatikan gambar berikut. Panjang CD = AC = 21 cm dan luas △ ABC = 294 cm 2 . Panjang BE adalah ....

5.0

Jawaban terverifikasi

Tanya ke AiRIS