Pertanyaan

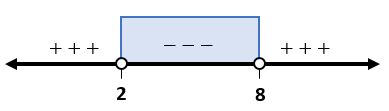
Apabila grafik y = k x 2 + ( k − 4 ) x + 2 1 seluruhnya di atas sumbu X, maka nilai k tidak mungkin sama dengan . . . .

Apabila grafik $y = k x^{2} + (k - 4) x + \frac{1}{2}$ seluruhnya di atas sumbu X, maka nilai $k$ tidak mungkin sama dengan . . . .

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

N. Puspita

Master Teacher

Jawaban terverifikasi

Jawaban

jawaban yang benar adalah A.

Pembahasan

Syarat agar nilai dari parabola selalu positif (di atas sumbu X) untuk semua nilai adalah dan (Definit Positif). Berdasarkan pernyataan di atas, maka batas nilai kagar parabola definit positif adalah: Buat pertidaksamaan menjadi persamaan kuadrat sehingga diperoleh solusi untuk . Selanjutnya, gunakan garis bilangan dan lakukan uji titik untuk memperoleh penyelesaiaan pertidaksamaan dari sebagai berikut: Dengan demikian, nilai kyang memenuhiadalah . Perhatikan opsi jawaban, yang tidak memenuhi nilai k pada interval adalah . Oleh karena itu, jawaban yang benar adalah A.

Syarat agar nilai dari parabola selalu positif (di atas sumbu X) untuk semua nilai adalah a greater than 0 dan D less than 0 (Definit Positif).

Berdasarkan pernyataan di atas, maka batas nilai k agar parabola y equals k x squared plus left parenthesis k minus 4 right parenthesis x plus 1 half definit positif adalah:

table attributes columnalign right center left columnspacing 0px end attributes row a greater than 0 row k greater than 0 end table

Buat pertidaksamaan menjadi persamaan kuadrat sehingga diperoleh solusi untuk .

Selanjutnya, gunakan garis bilangan dan lakukan uji titik untuk memperoleh penyelesaiaan pertidaksamaan dari sebagai berikut:

Dengan demikian, nilai k yang memenuhi adalah 2 less than k less than 8 .

Perhatikan opsi jawaban, yang tidak memenuhi nilai k pada interval 2 less than k less than 8 adalah k equals 1 1 half .

Oleh karena itu, jawaban yang benar adalah A.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.2 (4 rating)

Sey

Ini yang aku cari!

Abigail Alfiani Ros Angelina Simamora

Saya kurang paham, tapi penjelasannya sudah sangat lengkap

Pertanyaan serupa

Himpunan penyelesaian dari pertidaksamaan x 2 − 6 x + 8 ≥ 0 adalah ....

3.6

Jawaban terverifikasi

Penyelesaian dari pertidaksamaan kuadrat 4 x 2 + 5 x − 6 ≤ 0 adalah...

0.0

Jawaban terverifikasi

Himpunan penyelesaian dari pertidaksamaan kuadrat 2 x 2 + 7 x − 4 ≥ 0 adalah...

0.0

Jawaban terverifikasi

Tentukan penyelesaian pertidaksamaan 3 x 2 + 5 x − 2 ≤ 0 .

0.0

Jawaban terverifikasi

solusi pertaksamaan 2 x 2 + 3 x − 9 ≤ 0 yang bukan solusi dari pertidaksamaan 2 x 2 − x − 10 ≤ 0 adalah....

4.0

Jawaban terverifikasi

RUANGGURU HQ

Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860

Coba GRATIS Aplikasi Roboguru

Coba GRATIS Aplikasi Ruangguru

Produk Ruangguru

Produk Lainnya

Bantuan & Panduan

Hubungi Kami

+62 815-7441-0000

[email protected]

02140008000

Ikuti Kami

Apabila grafik y = k x 2 + ( k − 4 ) x + 2 1 ​ seluruhnya di atas sumbu X, maka nilai k tidak mungkin sama dengan . . . .

Jawaban

jawaban yang benar adalah A.

Pembahasan

Pertanyaan serupa

Apabila grafik y = k x 2 + ( k − 4 ) x + 2 1 seluruhnya di atas sumbu X, maka nilai k tidak mungkin sama dengan . . . .