Uswatun N
08 Maret 2024 02:24
Iklan
Uswatun N
08 Maret 2024 02:24
Pertanyaan
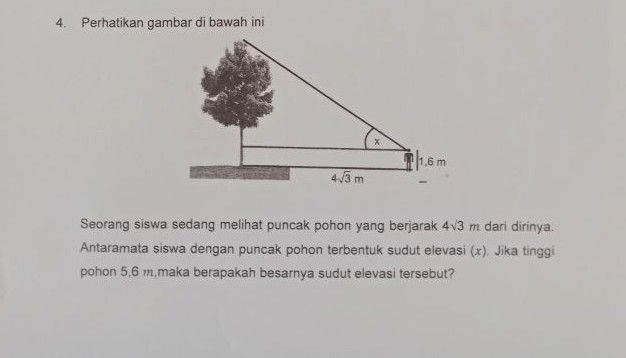
Seorang siswa sedang melihat puncak pohon yang berjarak 4√3 m dari dirinya. Antaramata siswa dengan puncak pohon terbentuk sudut elevasi (x). Jika tinggi pohon 5,6 m, maka berapakah besarnya sudut elevasi tersebut?
Seorang siswa sedang melihat puncak pohon yang berjarak 4√3 m dari dirinya. Antaramata siswa dengan puncak pohon terbentuk sudut elevasi (x). Jika tinggi pohon 5,6 m, maka berapakah besarnya sudut elevasi tersebut?
2
1
Iklan
Bakwan G
09 Maret 2024 01:18
<p>Besar sudut elevasinya adalah <strong>30°</strong></p><p> </p><p><strong>Diketahui :</strong></p><p>Jarak siswa dengan pohon = 4√3 m</p><p>Tinggi pohon = 5,6 m</p><p>Tinggi siswa = 1,6 m</p><p><strong>Ditanya : </strong>sudut elevasi = (x) = ... ?</p><p><strong>Jawab :</strong></p><p>Mencari sudut elevasinya menggunakan tangen :</p><p>tan (x) = (depan)÷(samping)</p><p> </p><p>Mencari panjang depan segitiga :</p><p>depan = tinggi pohon - tinggi siswa</p><p>depan = 5,6 m - 1,6 m</p><p>depan = 4,0 m</p><p> </p><p>Mencari panjang samping segitiga :</p><p>Jarak siswa dengan pohon = 4√3 m</p><p>samping = 4√3 m</p><p> </p><p>Masukan panjang depan dan samping segitiga ke rumus tangen :</p><p>tan (x) = (depan)÷(samping)</p><p>tan (x) = (4,0 m)÷(4√3 m)</p><p>tan (x) = ⅓√3 </p><p> (x) = 30°</p><p>Maka besar sudut elevasinya adalah 30°</p><p> </p><p>Selesai :D 🙏</p><p>Sumber : https://ngajimatematika.blogspot.com/2017/08/rangkuman-materi-trigonometri-dan.html?m=1</p>
Besar sudut elevasinya adalah 30°
Diketahui :
Jarak siswa dengan pohon = 4√3 m
Tinggi pohon = 5,6 m
Tinggi siswa = 1,6 m
Ditanya : sudut elevasi = (x) = ... ?
Jawab :
Mencari sudut elevasinya menggunakan tangen :
tan (x) = (depan)÷(samping)
Mencari panjang depan segitiga :
depan = tinggi pohon - tinggi siswa
depan = 5,6 m - 1,6 m
depan = 4,0 m
Mencari panjang samping segitiga :
Jarak siswa dengan pohon = 4√3 m
samping = 4√3 m
Masukan panjang depan dan samping segitiga ke rumus tangen :
tan (x) = (depan)÷(samping)
tan (x) = (4,0 m)÷(4√3 m)
tan (x) = ⅓√3
(x) = 30°
Maka besar sudut elevasinya adalah 30°
Selesai :D 🙏
Sumber : https://ngajimatematika.blogspot.com/2017/08/rangkuman-materi-trigonometri-dan.html?m=1
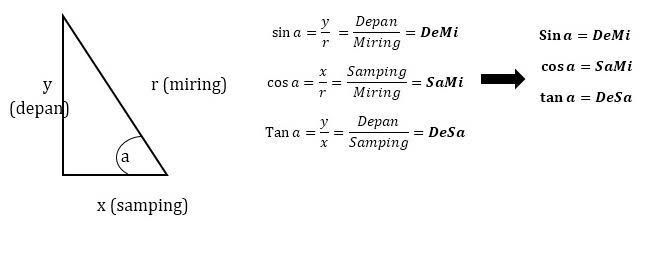
· 5.0 (1)
Uswatun N
28 Mei 2024 23:24
terimakasih
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



