Rini S
13 Januari 2023 09:40
Iklan
Rini S
13 Januari 2023 09:40
Pertanyaan
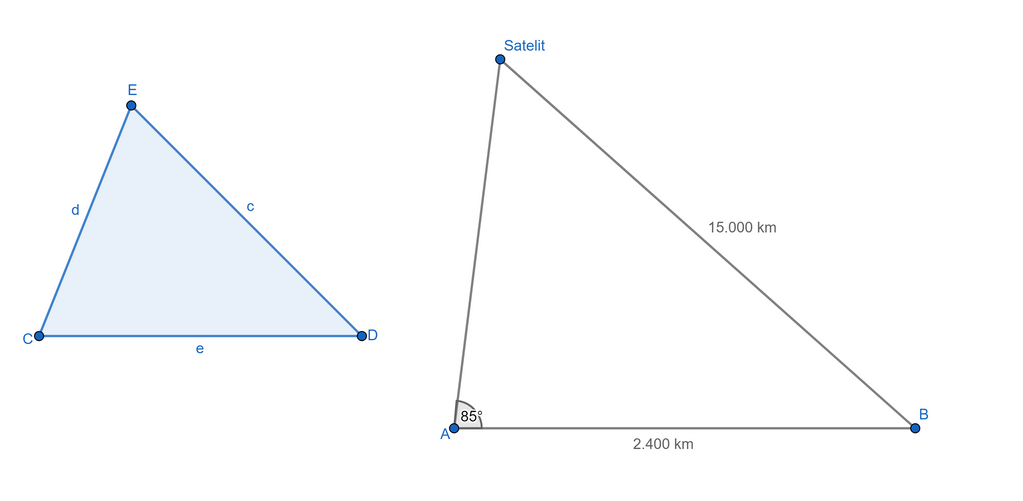
Sebuah satelit televisi berada diantara kota A dan kota B. Jarak antara kota A dan kota B adalah 2400 km. Untuk mendapatkan sinyal yang maksimal dari satelit televisi tersebut maka antena televisi yang terletak di kota A diatur menghadap satelit tersebut dengan sudut elevasi 85°. Jika jarak dari satelit televisi ke kota B adalah 15000 km, hitunglah luas segitiga yang terbentuk!
1
1
Iklan
S. SheilaTeacherAssisstant
Mahasiswa/Alumni Universitas Pancasila
30 Januari 2023 05:46
<p><strong>Jawaban: 17.951.859,64 km²</strong></p><p> </p><p><strong>Ingat!</strong></p><p><strong>Pada segitiga sembarang (lihat gambar), berlaku:</strong></p><p><strong>c² = d² + e² – 2 de cos C (Aturan Cosinus)</strong></p><p><strong>L ΔCDE = ½ de sin C (Aturan Sinus untuk Luas Segitiga)</strong></p><p><strong>Rumus abc persamaan kuadrat ax² + bx + c = 0:</strong></p><p><strong>x₁₂ = [-b ± √(b² – 4ac)]/2a</strong></p><p> </p><p>Sehingga, berdasarkan soal (lihat gambar), dapat diketahui bahwa AB = 2.400 km, ∠A = 85°, B-Satelit = 15.000 km.</p><p><strong>Untuk mencari luas segitiga, karena hanya satu sudut yang diketahui, gunakan Aturan Cosinus untuk mencari jarak A-Satelit terlebih dahulu:</strong></p><p><strong>(B-Satelit)² = (AB)² + (A-Satelit)² – 2 (AB)(A-Satelit)(cos A)</strong></p><p>15.000² = 2.400² + (A-Satelit)² – 2 (2.400)(A-Satelit)(cos 85°)</p><p>225.000.000 = 5.760.000 + (A-Satelit)² – (4.800)(A-Satelit)(0,087)</p><p>225.000.000 = 5.760.000 + (A-Satelit)² – (417,6)(A-Satelit)</p><p>Misalkan A-satelit = x, maka</p><p>x² – 417,6x + 5.760.000 – 225.000.000 = 0</p><p>x² – 417,6x – 219.240.000 = 0</p><p> </p><p><strong>Karena angkanya besar, maka gunakan rumus abc untuk mencari nilai x, dengan a = 1, b = -417,6, dan c = -219.240.000</strong></p><p><strong>x₁₂ = [-b ± √(b² – 4ac)]/2a</strong></p><p>x₁₂ = {-(-417,6 ± √[(-417,6)² – 4∙1∙(-219.240.000)]}/(2∙1)</p><p>x₁₂ = [417,6 ± √(174.389,76 + 876.960.000)]/2</p><p>x₁₂ = (417,6 ± √877.134.389,76)/2</p><p>x₁ = (417,6 + √877.134.389,76)/2</p><p>x₁ = 15.017,03 km</p><p>x₂ = (417,6 – √877.134.389,76)/2</p><p>x₂ = -14.599, 43 (tidak memenuhi karena jarak tidak negatif)</p><p><strong>Maka A-Satelit = 15.017,03 km</strong></p><p> </p><p><strong>Jadi, luas segitiga yang dibentuk oleh AB-Satelit dapat dicari dengan:</strong></p><p>L = ½ (AB)(A-Satelit) sin A</p><p>L = ½ (2.400)(15.017,03)(sin 85°)</p><p>L = ½ (2.400)(15.017,03)(0,996)</p><p><strong>L = 17.951.859,64 km²</strong></p><p> </p><p><strong><u>Dengan demikian, luas segitiga yang terbentuk adalah 17.951.859,64 km².</u></strong></p>
Jawaban: 17.951.859,64 km²
Ingat!
Pada segitiga sembarang (lihat gambar), berlaku:
c² = d² + e² – 2 de cos C (Aturan Cosinus)
L ΔCDE = ½ de sin C (Aturan Sinus untuk Luas Segitiga)
Rumus abc persamaan kuadrat ax² + bx + c = 0:
x₁₂ = [-b ± √(b² – 4ac)]/2a
Sehingga, berdasarkan soal (lihat gambar), dapat diketahui bahwa AB = 2.400 km, ∠A = 85°, B-Satelit = 15.000 km.
Untuk mencari luas segitiga, karena hanya satu sudut yang diketahui, gunakan Aturan Cosinus untuk mencari jarak A-Satelit terlebih dahulu:
(B-Satelit)² = (AB)² + (A-Satelit)² – 2 (AB)(A-Satelit)(cos A)
15.000² = 2.400² + (A-Satelit)² – 2 (2.400)(A-Satelit)(cos 85°)
225.000.000 = 5.760.000 + (A-Satelit)² – (4.800)(A-Satelit)(0,087)
225.000.000 = 5.760.000 + (A-Satelit)² – (417,6)(A-Satelit)
Misalkan A-satelit = x, maka
x² – 417,6x + 5.760.000 – 225.000.000 = 0
x² – 417,6x – 219.240.000 = 0
Karena angkanya besar, maka gunakan rumus abc untuk mencari nilai x, dengan a = 1, b = -417,6, dan c = -219.240.000
x₁₂ = [-b ± √(b² – 4ac)]/2a
x₁₂ = {-(-417,6 ± √[(-417,6)² – 4∙1∙(-219.240.000)]}/(2∙1)
x₁₂ = [417,6 ± √(174.389,76 + 876.960.000)]/2
x₁₂ = (417,6 ± √877.134.389,76)/2
x₁ = (417,6 + √877.134.389,76)/2
x₁ = 15.017,03 km
x₂ = (417,6 – √877.134.389,76)/2
x₂ = -14.599, 43 (tidak memenuhi karena jarak tidak negatif)
Maka A-Satelit = 15.017,03 km
Jadi, luas segitiga yang dibentuk oleh AB-Satelit dapat dicari dengan:
L = ½ (AB)(A-Satelit) sin A
L = ½ (2.400)(15.017,03)(sin 85°)
L = ½ (2.400)(15.017,03)(0,996)
L = 17.951.859,64 km²
Dengan demikian, luas segitiga yang terbentuk adalah 17.951.859,64 km².
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



