Vincensius F
22 Agustus 2023 09:27
Iklan
Vincensius F
22 Agustus 2023 09:27
Pertanyaan
Sebuah balok ABCD.EFGH mempunyai alas berbentuk persegi dengan Panjang sisi 3 cm dan tinggi 5 cm. Titik P terletak pada AD sehingga AP: PD = 1:2. Titik Q terletak pada FG dengan FQ: QG = 2:1. Tentukan jarak titik P ke titik Q
Sebuah balok ABCD.EFGH mempunyai alas berbentuk persegi dengan Panjang sisi 3 cm dan tinggi 5 cm. Titik P terletak pada AD sehingga AP: PD = 1:2. Titik Q terletak pada FG dengan FQ: QG = 2:1. Tentukan jarak titik P ke titik Q
3
2
Iklan
Ab C
22 Agustus 2023 10:32
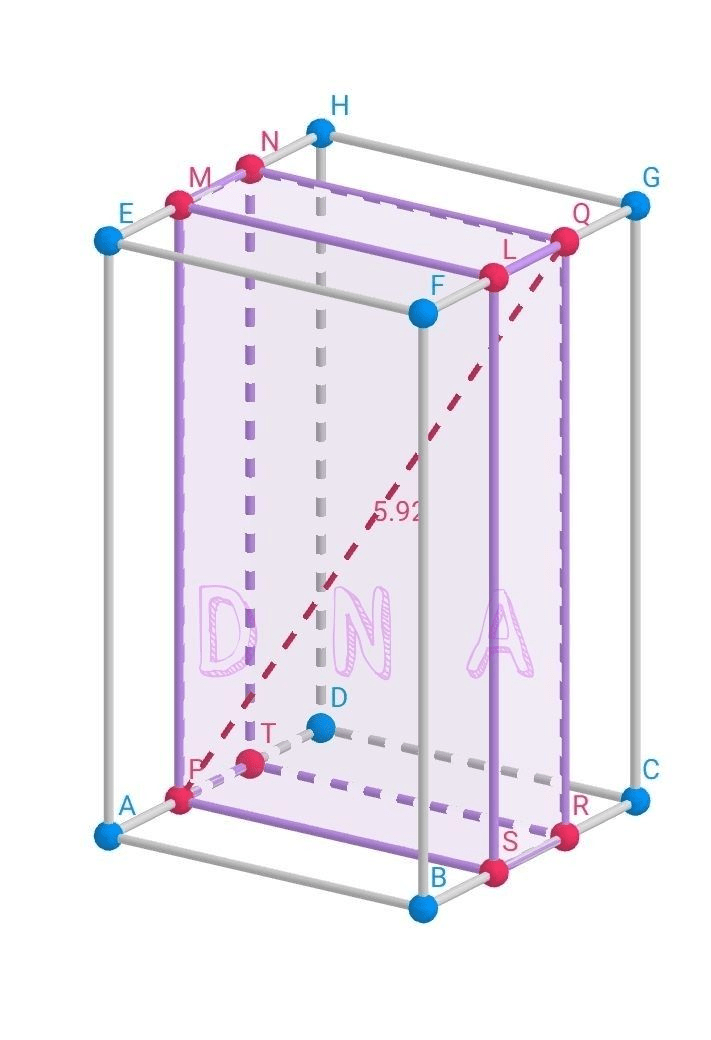
<p>Balok</p><p>AB = BC = 3 cm</p><p>AE = 5 cm</p><p> </p><p>P pada AD</p><p>AP : PD = 1 : 2</p><p>AP = AD × 1/(1 + 2) = 3 × 1/3 = 1 cm</p><p> </p><p>Q pada FG</p><p>FQ : QG = 2 : 1</p><p>FQ = FG × 2/(2 + 1) = 3 × 2/3 = 2 cm</p><p> </p><p><strong>Perhatikan balok PSRT.MLQN</strong></p><p> </p><p><strong>Jarak titik P ke titik Q</strong></p><p>= diagonal ruang balok PSRT.MLQN</p><p>= √(PS² + SR² + RQ²)</p><p>= √(3² + 1² + 5²)</p><p>= √(9 + 1 + 25)</p><p>= <strong>√35 cm</strong></p><p>≈ 5,92 cm</p><p> </p>
Balok
AB = BC = 3 cm
AE = 5 cm
P pada AD
AP : PD = 1 : 2
AP = AD × 1/(1 + 2) = 3 × 1/3 = 1 cm
Q pada FG
FQ : QG = 2 : 1
FQ = FG × 2/(2 + 1) = 3 × 2/3 = 2 cm
Perhatikan balok PSRT.MLQN
Jarak titik P ke titik Q
= diagonal ruang balok PSRT.MLQN
= √(PS² + SR² + RQ²)
= √(3² + 1² + 5²)
= √(9 + 1 + 25)
= √35 cm
≈ 5,92 cm
· 0.0 (0)
Iklan
Faiz D
Community
14 Oktober 2023 15:15
<p>Untuk menentukan jarak antara titik P dan Q, kita akan menggunakan proporsi dari perbandingan AP:PD dan FQ:QG. Kemudian, kita akan menggunakan teorema Pythagoras untuk menghitung jaraknya.</p><p> </p><p>Pertama, kita harus menemukan titik koordinat P dan Q dalam sistem koordinat. Mari kita sebut titik A (0,0) sebagai titik awal. Diketahui bahwa AP:PD = 1:2, jadi titik P adalah 1/3 dari panjang AD, dan titik Q adalah 2/3 dari panjang FG.</p><p> </p><p>Panjang AD adalah 3 cm, jadi koordinat titik P adalah (1/3 * 3 cm, 0) = (1 cm, 0). Panjang FG juga adalah 3 cm, jadi koordinat titik Q adalah (2/3 * 3 cm, 5 cm) = (2 cm, 5 cm).</p><p> </p><p>Sekarang, kita dapat menghitung jarak antara titik P (1,0) dan Q (2,5) dengan menggunakan teorema Pythagoras:</p><p>Jarak PQ = √((x2 - x1)^2 + (y2 - y1)^2) Jarak PQ = √((2 - 1)^2 + (5 - 0)^2) Jarak PQ = √(1 + 25) Jarak PQ = √26 cm</p><p> </p><p><strong>Jadi, jarak antara titik P dan Q adalah √26 cm.</strong></p>
Untuk menentukan jarak antara titik P dan Q, kita akan menggunakan proporsi dari perbandingan AP:PD dan FQ:QG. Kemudian, kita akan menggunakan teorema Pythagoras untuk menghitung jaraknya.
Pertama, kita harus menemukan titik koordinat P dan Q dalam sistem koordinat. Mari kita sebut titik A (0,0) sebagai titik awal. Diketahui bahwa AP:PD = 1:2, jadi titik P adalah 1/3 dari panjang AD, dan titik Q adalah 2/3 dari panjang FG.
Panjang AD adalah 3 cm, jadi koordinat titik P adalah (1/3 * 3 cm, 0) = (1 cm, 0). Panjang FG juga adalah 3 cm, jadi koordinat titik Q adalah (2/3 * 3 cm, 5 cm) = (2 cm, 5 cm).
Sekarang, kita dapat menghitung jarak antara titik P (1,0) dan Q (2,5) dengan menggunakan teorema Pythagoras:
Jarak PQ = √((x2 - x1)^2 + (y2 - y1)^2) Jarak PQ = √((2 - 1)^2 + (5 - 0)^2) Jarak PQ = √(1 + 25) Jarak PQ = √26 cm
Jadi, jarak antara titik P dan Q adalah √26 cm.
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu
LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian
Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!
