Resha A
26 Juni 2022 12:01
Iklan
Resha A
26 Juni 2022 12:01
Pertanyaan
Perhatikan gambar di bawah ini. CD : DB = 3 : 5, AE : EB = 4 : 1. Jika vektor(AB) = vektor (a) dan vektor (AC) = vektor (b), maka vektor (AP) = ... A. (8)/(35)(3 vec(a)+5 vec(b)) B. (4)/(35)(3 vec(a)+5 vec(b)) C. (6)/(35)(3 vec(a)+5 vec(b)) D. (3)/(35)(3 vec(a)+5 vec(b)) E. (5)/(35)(3 vec(a)+5 vec(b))
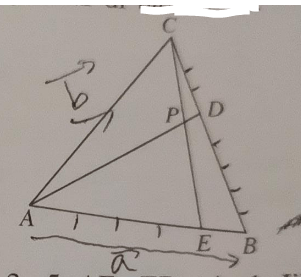
6
1
Iklan
T. Teaching.Assistant.Yosi
Master Teacher
01 Maret 2023 06:49
<p>Jawaban : B. (4)/(35)(3 vec(a)+5 vec(b))</p><p> </p><p>Pembahasan :</p><p>Gunakan beberapa konsep berikut :</p><p>1. Dalil Menelaus: </p><p>BE/EC · CD/DA · AF/FB = 1 </p><p>2. Konsep perbandingan vektor dalam: Titik P berada pada AB dengan perbandingan AP:PB = m:n, maka p = (mb+na)/(m+n) dengan a adalah vektor OA, b adalah vektor OB, dan p adalah vektor OP. </p><p>3. AB = AC + CB</p><p> </p><p>Diketahui : </p><p>CD : DB = 3 : 5 </p><p>DB = 5/3 CD</p><p>Sehingga CB = CD+DB </p><p>CB = CD+5/3 CD </p><p>CB = 8/3 CD </p><p>CB/CD = 8/3 </p><p>AE : EB = 4:1 </p><p>AE/EB = 4/1 </p><p>Dengan menggunakan dalil Menelaus diperoleh </p><p>PD/AP · AE/EB · CB/CD = 1 </p><p>PD/AP · 4/1 · 8/3 = 1 </p><p>PD/AP · 32/3 = 1 </p><p>PD/AP = 3/32 </p><p>PD = 3/32 AP </p><p>Diketahui vektor AB = a vektor AC = b , titik D membagi CB dengan perbandingan CD : DB = 3 : 5, maka AD = (3a+5b)/(3+5) </p><p>AD = (3a+5b)/8 </p><p>AP+PD = AD</p><p>AP+PD = (3a+5b)/8 </p><p>AP+3/32 AP = (3a+5b)/8 </p><p>35/32 AP = (3a+5b)/8 </p><p>AP = (3a+5b)/8 . 32/35</p><p>AP = 4/35 (3a+5b)</p><p> </p><p>Jadi jawaban yang paling tepat adalah B.</p>
Jawaban : B. (4)/(35)(3 vec(a)+5 vec(b))
Pembahasan :
Gunakan beberapa konsep berikut :
1. Dalil Menelaus:
BE/EC · CD/DA · AF/FB = 1
2. Konsep perbandingan vektor dalam: Titik P berada pada AB dengan perbandingan AP:PB = m:n, maka p = (mb+na)/(m+n) dengan a adalah vektor OA, b adalah vektor OB, dan p adalah vektor OP.
3. AB = AC + CB
Diketahui :
CD : DB = 3 : 5
DB = 5/3 CD
Sehingga CB = CD+DB
CB = CD+5/3 CD
CB = 8/3 CD
CB/CD = 8/3
AE : EB = 4:1
AE/EB = 4/1
Dengan menggunakan dalil Menelaus diperoleh
PD/AP · AE/EB · CB/CD = 1
PD/AP · 4/1 · 8/3 = 1
PD/AP · 32/3 = 1
PD/AP = 3/32
PD = 3/32 AP
Diketahui vektor AB = a vektor AC = b , titik D membagi CB dengan perbandingan CD : DB = 3 : 5, maka AD = (3a+5b)/(3+5)
AD = (3a+5b)/8
AP+PD = AD
AP+PD = (3a+5b)/8
AP+3/32 AP = (3a+5b)/8
35/32 AP = (3a+5b)/8
AP = (3a+5b)/8 . 32/35
AP = 4/35 (3a+5b)
Jadi jawaban yang paling tepat adalah B.
· 0.0 (0)
Iklan
Buka akses jawaban yang telah terverifikasi

Yah, akses pembahasan gratismu habis
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia













