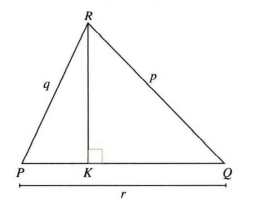
Pada gambar di atas diketahui: luas ΔMQR = Δluas PKR + luas ΔQKR. Gunakan rumus segitiga: L = (1/2)pq sin R untuk membuktikan bahwa sin (a + b) = sin a cos b + cos a sin b.

<p>Sebelumnya diasumsikan bahwa ∠PRK = a dan ∠QRK = b</p><p>Jawaban: terbukti bahwa sin (a + b) = sin a cos b + cos a sin b</p><p>&nbsp;</p><p>Ingat bahwa!</p><p>Aturan sinus luas segitiga</p><p>Pada segitiga sebarang ABC maka berlaku</p><p>L=½ × a × b × sin C</p><p>L=½ × b × c × sin A</p><p>L=½ × a × c × sin C</p><p>sin 𝞪 = sisi di depan sudut/ sisi miring</p><p>cos 𝞪 = sisi di dekat sudut/sisi miring</p><p>&nbsp;</p><p>Berdasarkan aturan sinus tentang mencari luas maka&nbsp;</p><p>luas ΔPRK = ½ × q × RK × sin a</p><p>luas ΔQRK = ½ × p × RK × sin b</p><p>luas ΔPQR = ½ × p × q × sin (a+b)</p><p>&nbsp;</p><p>Berdasarkan gambar diperoleh</p><p>luas ΔPQR = luas ΔPRK +luas ΔQRK</p><p>½ × p × q × sin (a+b)=½ × q × RK × sin a +½ × p × RK × sin b</p><p>&nbsp;p × q × sin (a+b) = &nbsp;q × RK × sin a +p × RK × sin b</p><p>sin (a+b) = (q × RK × sin a +p × RK × sin b):( p × q)</p><p>sin (a+b) = (RK × sin a)/p +(RK × sin b)/q</p><p>sin (a+b) = RK/p &nbsp;× sin a &nbsp;+ RK/q × sin b</p><p>&nbsp;</p><p>cos a = RK/q</p><p>cos b = RK/p</p><p>sehingga</p><p>sin (a+b) = RK/p &nbsp;× sin a &nbsp;+ RK/q × sin b</p><p>sin (a+b) = cos b &nbsp;× sin a &nbsp;+ cos a × sin b</p><p>sin (a+b) = sin a cos b + cos a sin b (terbukti)</p><p>&nbsp;</p><p>Jadi, berdasarkan hitungan di atas terbukti bahwa sin (a+b) = sin a cos b + cos a sin b.</p>