Marina S
06 Desember 2022 01:12
Iklan
Marina S
06 Desember 2022 01:12
Pertanyaan
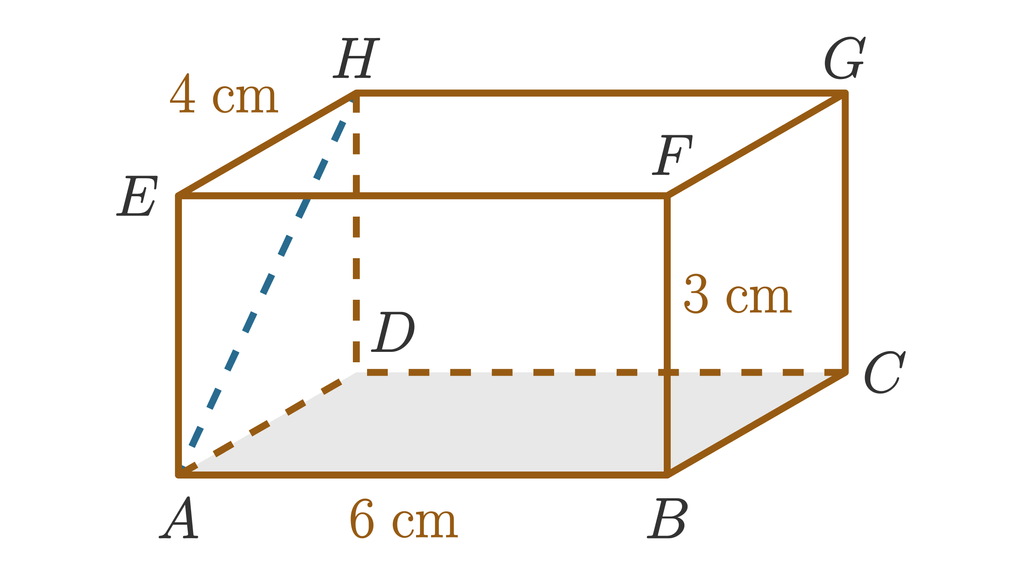
Pada balok ABCDEFGH diketahui : Panjang balok EH = 4 cm, panjang BF = 3 cm, dan panjang AB = 6 cm, maka : Tentukan panjang EA dan panjang AH !
1
1
Iklan
R. Nurhayati
Mahasiswa/Alumni Universitas Negeri Semarang
04 Januari 2023 13:17
<p>Jawaban: EA = 3 cm dan AH = 5 cm.</p><p> </p><p>Ingat:</p><p>Balok adalah bangun ruang sisi datar yang memiliki tiga pasang sisi berbentuk persegi panjang saling berhadapan.</p><p>Pada segitiga siku-siku dengan panjang sisi tegaknya a dan b, serta panjang sisi miringnya c, berlaku rumus pythagoras:</p><p>c<sup>2</sup> = a<sup>2</sup> + b<sup>2</sup>.</p><p> </p><p>Diketahui balok ABCD.EFGH dengan ukuran panjang EH = 4 cm, panjang BF = 3 cm, dan panjang AB = 6 cm.</p><p>Karena EA adalah tinggi balok, maka EA = BF = 3 cm.</p><p> </p><p>Perhatikan segitiga siku-siku yang terbentuk AEH pada gambar di bawah.</p><p>Maka berlaku:</p><p>AH<sup>2</sup> = AE<sup>2</sup> + EH<sup>2</sup></p><p>AH<sup>2</sup> = (3)<sup>2</sup> + (4)<sup>2</sup></p><p>AH<sup>2</sup> = 9 + 16</p><p>AH<sup>2</sup> = 25</p><p> AH = ± √25</p><p> AH = ± 5</p><p>Karena AH adalah panjang diagonal sisi maka nilainya selalu positif, AH = 5 cm.</p><p> </p><p>Jadi, panjang EA = 3 cm dan AH = 5 cm.</p>
Jawaban: EA = 3 cm dan AH = 5 cm.
Ingat:
Balok adalah bangun ruang sisi datar yang memiliki tiga pasang sisi berbentuk persegi panjang saling berhadapan.
Pada segitiga siku-siku dengan panjang sisi tegaknya a dan b, serta panjang sisi miringnya c, berlaku rumus pythagoras:
c2 = a2 + b2.
Diketahui balok ABCD.EFGH dengan ukuran panjang EH = 4 cm, panjang BF = 3 cm, dan panjang AB = 6 cm.
Karena EA adalah tinggi balok, maka EA = BF = 3 cm.
Perhatikan segitiga siku-siku yang terbentuk AEH pada gambar di bawah.
Maka berlaku:
AH2 = AE2 + EH2
AH2 = (3)2 + (4)2
AH2 = 9 + 16
AH2 = 25
AH = ± √25
AH = ± 5
Karena AH adalah panjang diagonal sisi maka nilainya selalu positif, AH = 5 cm.
Jadi, panjang EA = 3 cm dan AH = 5 cm.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



