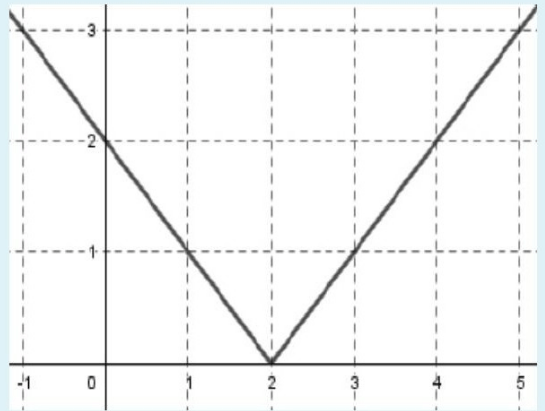
Grafik fungsi nilai mutlak pada gambar di bawah ini adalah .... a. f(x)=|2x−2| b. f(x)=|x−3| c. f(x)=|2x−3| d. f(x)=|x−2| e. f(x)=|x+3|

Jawaban yang benar adalah D. f(x) = |x-2|. Pembahasan. Konsep: Nilai mutlak adalah suatu jarak bilangan itu dengan nol, dan nilai mutlak selalu bernilai positif, Bentuk umum nilai mutlak |x| = x, jika x ≥ 0 |x| = -x, jika x < 0 Untuk menggambar grafik nilai mutlak kita ambil sebarang nilai x, kemudian kita uji ke persamaan yang diketahui. Kita ambil nilai x = (-1, 0, 1, 2, 3, 4, 5), kita uji nilai x ke masing-masing persamaan nilai mutlak yang diketahui > f(x)=|2x−2|, dimana nilai x = -1, 0, 1, 2, 3, 4, 5, maka f(-1) = |2(-1)−2| = |-2−2| = |−4| = 4, diperoleh (-1,4) f(0) = |2(0)−2| = |0−2| = |−2| = 2, diperoleh (0,2) f(1) = |2(1)−2| = |2−2| = |0| = 0, diperoleh (1,0) f(2) = |2(2)−2| = |4−2| = |2| = 2, diperoleh (2,2) f(3) = |2(3)−2| = |6−2| = |4| = 4, diperoleh (3,4) f(4) = |2(4)−2| = |8−2| = |6| = 6, diperoleh (4,6) f(5) = |2(5)−2| = |10−2| = |8| = 8, diperoleh (5,8) (Salah karena berbeda pada gambar titik yang diketahui adalah ((-1,3), (0,2), (1,1), (2, 0), (3,1), (4,2), (5,3)) b. f(x)=|x−3| f(-1) = |(-1)−3| = |−4| = 4, diperoleh (-1,4) f(0) = |(0)−3| = |−3| = 3, diperoleh (0,3) f(1) = |(1)−3| = |-2| = 2, diperoleh (1,2) f(2) = |(2)−3| = |-1| = 1, diperoleh (2,1) f(3) = |(3)−3| = |0| = 0, diperoleh (3,0) f(4) = |(4)−3| = |1| = 1, diperoleh (4,1) f(5) = |(5)−3| = |2| = 2, diperoleh (5,2) (Salah karena berbeda pada gambar titik yang diketahui adalah ((-1,3), (0,2), (1,1), (2, 0), (3,1), (4,2), (5,3)) c. f(x)=|2x−3| f(-1) = |2(-1)−3| = |-2−3| = |−5| = 5, diperoleh (-1,5) f(0) = |2(0)−3| = |0−3| = |−3| = 3, diperoleh (0,3) f(1) = |2(1)−3| = |2−3| = |-1| = 1, diperoleh (1,1) f(2) = |2(2)−3| = |4−3| = |1| = 1, diperoleh (2,1) f(3) = |2(3)−3| = |6−3| = |3| = 3, diperoleh (3,3) f(4) = |2(4)−3| = |8−3| = |5| = 5, diperoleh (4,5) f(5) = |2(5)−3| = |10−3| = |7| = 7, diperoleh (5,7) (Salah karena berbeda pada gambar titik yang diketahui adalah ((-1,3), (0,2), (1,1), (2, 0), (3,1), (4,2), (5,3)) d. f(x)=|x−2| f(-1) = |(-1)−2| = |−3| = 3, diperoleh (-1,3) f(0) = |(0)−2| = |−2| = 2, diperoleh (0,2) f(1) = |(1)−2| = |-1| = 1, diperoleh (1,1) f(2) = |(2)−2| = |0| = 0, diperoleh (2,0) f(3) = |(3)−2| = |1| = 1, diperoleh (3,1) f(4) = |(4)−2| = |2| = 2, diperoleh (4,2) f(5) = |(5)−2| = |3| = 3, diperoleh (5,3) (Benar karena sesuai pada gambar titik yang diketahui adalah ((-1,3), (0,2), (1,1), (2, 0), (3,1), (4,2), (5,3)) e. f(x)=|x+3| f(-1) = |(-1)+3| = |2| = 2, diperoleh (-1,2) f(0) = |(0)+3| = |3| = 3, diperoleh (0,3) f(1) = |(1)+3| = |4| = 4, diperoleh (1,4) f(2) = |(2)+3| = |5| = 5, diperoleh (2,5) f(3) = |(3)+3| = |6| = 6, diperoleh (3,6) f(4) = |(4)+3| = |7| = 7, diperoleh (4,7) f(5) = |(5)+3| = |8| = 8, diperoleh (5,8) (Salah karena berbeda pada gambar titik yang diketahui adalah ((-1,3), (0,2), (1,1), (2, 0), (3,1), (4,2), (5,3)) Jadi, dariu pengujian titik-titik diatas, maka grafik di atas merupakan grafik fungsi nilai mutlak f(x)=|x−2|. Oleh karena itu jawaban yang benar adalah D. f(x)=|x−2|.