Gambarlah sketsa grafik dari setiap fungsi kuadrat f(x) = x² - 6x +g dengan domain (Df) = {x |o < x ≤ 5,XER} lalu tentukan daerah hasilnya.

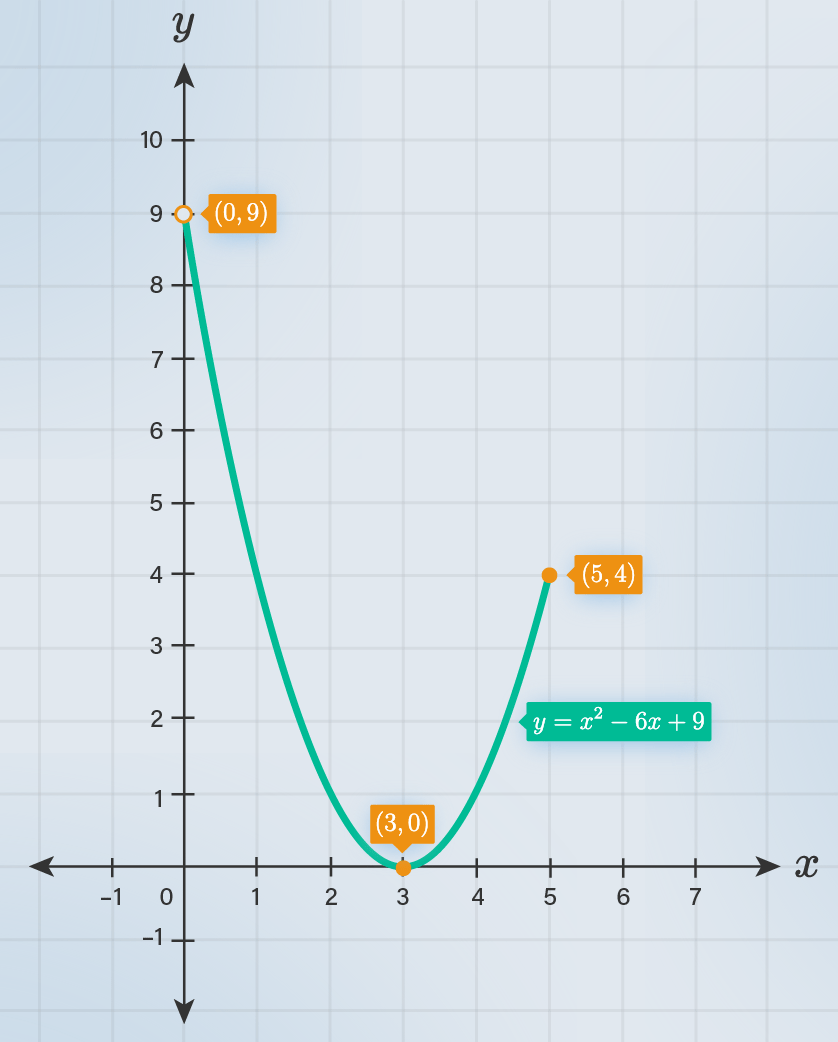
Halo Martin, terima kasih sudah bertanya di Roboguru. Jawaban untuk soal diatas ada pada gambar terlampir dengan daerah hasil atau Rf = {y| 0 ≤ y < 9, x ∈ ℝ}. Untuk menggambar fungsi kuadrat f(x) = ax² + bx + c, minimal diperlukan tiga titik yaitu: ▸Titik potong sumbu-x saat y = 0 ▸Titik potong sumbu-y saat x = 0 ▸Titik puncak fungsi kuadrat (xp, yp) = (-b/2a, (b² - 4ac)/-4a) Asumsi fungsi kuadrat f(x) = x² - 6x + 9 dengan domain Df = {x| 0 < x ≤ 5, x ∈ ℝ} Diperoleh penyelesaiannya: ▸Titik potong sumbu-x saat y = 0 f(x) = x² - 6x + 9 0 = x² - 6x + 9 0 = (x - 3)(x - 3) x - 3 = 0 x = 3 Titik potong sumbu-x adalah (3, 0). ▸Titik potong sumbu-y saat x = 0 f(x) = x² - 6x + 9 f(0) = 0² - 6(0) + 9 f(0) = 0 - 0 + 9 f(0) = 9 Titik potong sumbu-y adalah (0, 9). ▸Titik puncak fungsi kuadrat f(x) = x² - 6x + 9, dengan a = 1, b = -6, dan c = 9. (xp, yp) = (-b/2a, (b² - 4ac)/-4a) (xp, yp) = (-(-6)/2(1), ((-6)² - 4(1)(9))/-4(1)) (xp, yp) = (6/2, (36 - 36)/-4) (xp, yp) = (3, 0/-4) (xp, yp) = (3, 0) Titik puncak fungsi kuadrat adalah (3, 0). Tentukan daerah hasil dengan substitusi daerah asal pada Df = {x| 0 < x ≤ 5, x ∈ ℝ}. ▸Untuk x = 0, maka: f(x) = x² - 6x + 9 f(0) = 0² - 6(0) + 9 f(0) = 0 - 0 + 9 f(0) = 9 ▸Untuk x = 1, maka: f(x) = x² - 6x + 9 f(1) = 1² - 6(1) + 9 f(1) = 1 - 6 + 9 f(1) = 4 ▸Untuk x = 2, maka: f(x) = x² - 6x + 9 f(2) = 2² - 6(2) + 9 f(2) = 4 - 12 + 9 f(2) = 1 ▸Untuk x = 3, maka: f(x) = x² - 6x + 9 f(3) = 3² - 6(3) + 9 f(3) = 9 - 18 + 9 f(3) = 0 ▸Untuk x = 4, maka: f(x) = x² - 6x + 9 f(4) = 4² - 6(4) + 9 f(4) = 16 - 24 + 9 f(4) = 1 ▸Untuk x = 5, maka: f(x) = x² - 6x + 9 f(5) = 5² - 6(5) + 9 f(5) = 25 - 30 + 9 f(5) = 4 Dengan demikian, daerah hasilnya adalah Rf = {y| 0 ≤ y < 9, x ∈ ℝ} dengan gambar terlampir.