Dinda D

25 November 2023 15:04
Iklan
Dinda D

25 November 2023 15:04
Pertanyaan
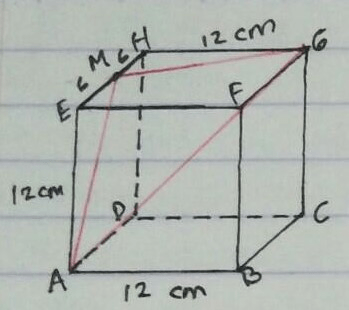
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm. Titik M terletak di pertengahan EH. Jarak titik M ke garis AG adalah ... cm
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm. Titik M terletak di pertengahan EH. Jarak titik M ke garis AG adalah ... cm
8
1
Iklan
BimBim B
26 November 2023 01:02
<h2><strong>Jawabannya adalah adalah 6√2 cm.</strong></h2><p> </p><p><strong><u>Penjelasan</u></strong></p><p>Posisi titik M dan garis AG pada kubus. Garis AG adalah garis yang menghubungkan titik A dan G, sedangkan titik M terletak di pertengahan EH.</p><p>Langkah-langkah untuk menemukan jarak titik M ke garis AG:</p><ol><li>Hitung panjang AM (panjang dari titik A ke titik M).</li><li>Hitung panjang MG (panjang dari titik M ke titik G).</li><li>Gunakan teorema Pythagoras untuk menemukan panjang jarak titik M ke garis AG.</li></ol><p>Panjang sisi kubus ABCD.EFGH adalah 12 cm. Oleh karena itu, panjang AM dan MG dapat dihitung sebagai setengah dari panjang sisi kubus.</p><ol><li><i>AM </i>= ½ × 12 = 6 cm</li><li><i>MG </i>= ½ × 12 = 6 cm</li></ol><p>Sekarang, kita dapat menggunakan teorema Pythagoras untuk menemukan panjang jarak <i>GM</i> (yang juga merupakan jarak titik M ke garis AG):</p><p><i>GM </i>= √(<i>AM</i><sup>2</sup>+<i>MG</i><sup>2</sup>)</p><p><i>GM </i>= √(6<sup>2</sup>+6<sup>2</sup>)</p><p><i>GM </i>= √(36+36)</p><p><i>GM </i>= √72</p><p><i>GM </i>= 6√2</p><p> </p><p><strong>Jadi, jarak titik M ke garis AG pada kubus ABCD.EFGH adalah 6√2 cm.</strong></p>
Jawabannya adalah adalah 6√2 cm.
Penjelasan
Posisi titik M dan garis AG pada kubus. Garis AG adalah garis yang menghubungkan titik A dan G, sedangkan titik M terletak di pertengahan EH.
Langkah-langkah untuk menemukan jarak titik M ke garis AG:
- Hitung panjang AM (panjang dari titik A ke titik M).
- Hitung panjang MG (panjang dari titik M ke titik G).
- Gunakan teorema Pythagoras untuk menemukan panjang jarak titik M ke garis AG.
Panjang sisi kubus ABCD.EFGH adalah 12 cm. Oleh karena itu, panjang AM dan MG dapat dihitung sebagai setengah dari panjang sisi kubus.
- AM = ½ × 12 = 6 cm
- MG = ½ × 12 = 6 cm
Sekarang, kita dapat menggunakan teorema Pythagoras untuk menemukan panjang jarak GM (yang juga merupakan jarak titik M ke garis AG):
GM = √(AM2+MG2)
GM = √(62+62)
GM = √(36+36)
GM = √72
GM = 6√2
Jadi, jarak titik M ke garis AG pada kubus ABCD.EFGH adalah 6√2 cm.
· 5.0 (1)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



