Dengan metode uji titik sudut, tentukan nilai optimum fungsi objektif dari program linear berikut: 2x+3y≥40 2x+2y≥28 8x+2y≥32 x,y≥0 dan x,y∈R Z=3x+4y

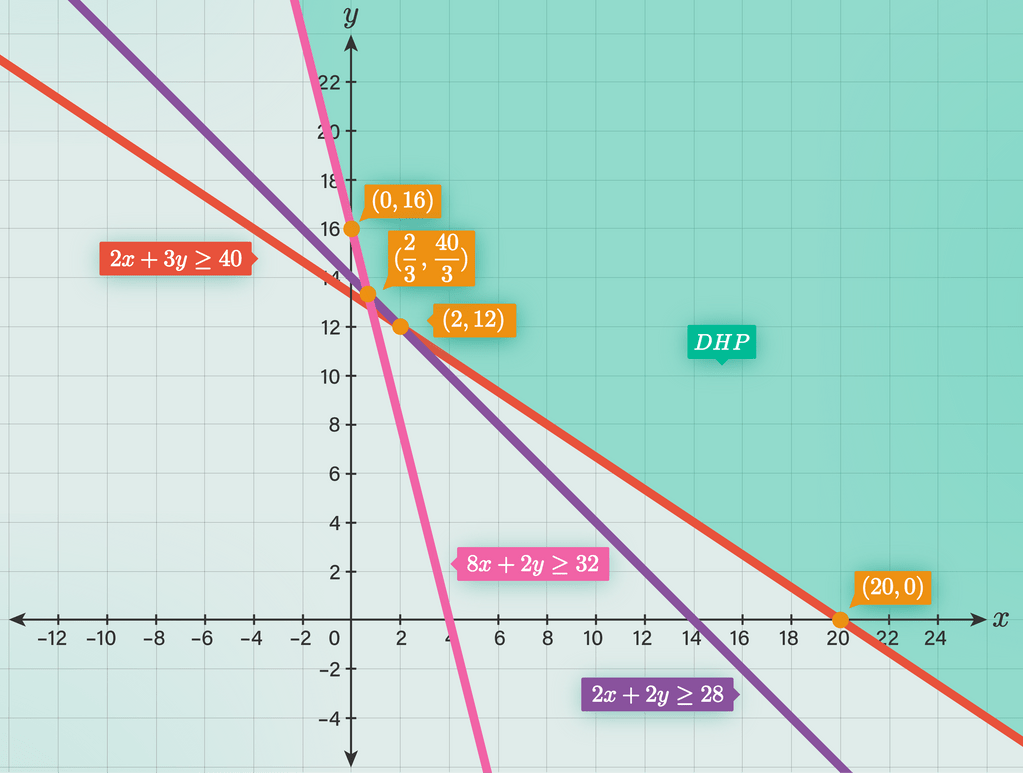
Halo Kania, kakak bantu jawab ya :) Jawaban : Minimum = 54 dan maksimum = 64 Ingat! Menggambarkan grafik fungsi linear yaitu dengan menentukan titik potongnya. 1. Menentukan titik potong dengan sumbu - x (y = 0) 2. Menentukan titik potong dengan sumbu - y (x = 0) ● Menggambar grafik 2x+3y ≥ 40 kita ubah dalam bentuk persamaan 2x+3y = 40. Titik potong dengan sumbu - x 2x + 0 = 40 2x = 40 x = 20 Koordinat titik potong : (20, 0) Titik potong dengan sumbu - y 0 + 3y = 40 3y = 40 y = 40/3 Koordinat titik potong : (0, 40/3) ● Menggambar grafik 2x+2y ≥ 28 kita ubah dalam bentuk persamaan 2x+2y=28 → x+y=14. Titik potong dengan sumbu - x x + 0 = 14 x = 14 Koordinat titik potong : (14, 0) Titik potong dengan sumbu - y 0 + y = 14 y = 14 Koordinat titik potong : (0, 14) ● Menggambar grafik 8x+2y ≥ 32 kita ubah dalam bentuk persamaan 8x+2y = 32. Titik potong dengan sumbu - x 8x + 0 = 32 8x = 32 x = 4 Koordinat titik potong : (4, 0) Titik potong dengan sumbu - y 0 + 2y = 32 2y = 32 y = 16 Koordinat titik potong : (0, 16) ● Menentukan DHP Uji titik misalkan (0,0) substitusikan pada pertidaksamaan-pertidaksamaan di atas. 2x+3y ≥ 40 0 + 0 ≥ 40 0 ≥ 40 (salah) → Arsir daerah yang tidak memuat titik (0,0) Karena 2x+2y ≥ 28 dan 8x+2y ≥ 32 memiliki tanda pertidaksamaan yang sama (≥) dengan 2x+3y ≥ 40, maka daerah yang diarsir juga daerah yang tidak memuat titik (0,0). Perhatikan kendala non negatif, x,y≥0, maka arsir daerah pada kuadran I. DHP pada gambar terlampir. ● Menentukan titik potong persamaan garis 8x+2y = 32 dan 2x+2y = 28. Eliminasi kedua persamaan. 8x + 2y = 32 2x + 2y = 28 ----------------- - 6x = 4 x = 4/6 x = 2/3 Substitusi x = 2/3 pada persamaan 2x+2y = 28 → x+y=14. (2/3)+y = 14 2 + 3y = 42 3y = 40 y = 40/3 Koordinat titik potong : (2/3, 40/3) ● Menentukan titik potong persamaan garis 2x+2y = 28 dan 2x+3y = 40. Eliminasi kedua persamaan. 2x + 3y = 40 2x + 2y = 28 -------------- - y = 12 Substitusi y = 12 pada persamaan 2x+2y = 28 → x+y=14. x + 12 = 14 x = 2 Koordinat titik potong : (2, 12) ● Uji titik pojok (sudut) Fungsi tujuan : Z = 3x+4y (0, 16) → Z = 0 + 4(16) = 64 (Maksimum) (2/3, 40/3) → Z = 3(2/3) + 4(40/3) = 6/3 + 160/3 = 166/3 (2, 12) → Z = 3(2) + 4(12) = 6 + 48 = 54 (Minimum) (20, 0) → Z = 3(20) + 4(0) = 60 Dengan demikian, nilai optimum fungsi objektif soal tersebut adalah 54 (minimum) dan 64 (maksimum).