Iklan
Pertanyaan
Tangki air dengan lubang kebocoran diperlihatkan gambar berikut. Jarak lubang ke tanah adalah 10 m dan jarak lubang ke permukaan air adalah 3,2 m. Tentukan: Kecepatan keluarnya air. Jarak mendatar terjauh yang dicapai air. Waktu yang diperlukan bocoran air untuk menyentuh tanah.
Tangki air dengan lubang kebocoran diperlihatkan gambar berikut.
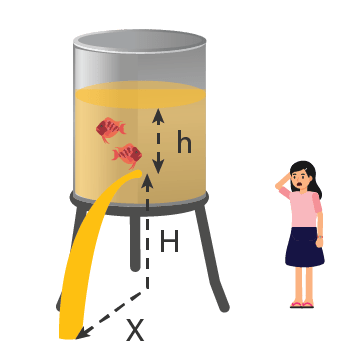
Jarak lubang ke tanah adalah 10 m dan jarak lubang ke permukaan air adalah 3,2 m. Tentukan:
- Kecepatan keluarnya air.
- Jarak mendatar terjauh yang dicapai air.
- Waktu yang diperlukan bocoran air untuk menyentuh tanah.
Iklan
YM
Y. Maghfirah
Master Teacher
Jawaban terverifikasi
21
4.6 (42 rating)
SD
Sekar Damayanti
Pembahasan lengkap banget
NF
Nayla FW
Pembahasan lengkap banget Mudah dimengerti Bantu banget Makasih ❤️
ZF
Zaira Firjannah
Pembahasan lengkap banget Ini yang aku cari! Mudah dimengerti Bantu banget Makasih ❤️
NN
Navya Naurah
Ini yang aku cari!
DD
Divtania Diva
Makasih ❤️
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia















