Pertanyaan

Sebuah tabung berisi penuh zat cair (ideal). Pada dindingnya sejauh 20 cm dari permukaan atas terdapat lubang kecil (jauh lebih kecil dari penampang tabung) sehingga zat cair memancar (terlihat seperti pada gambar). Besar kecepatan pancaran air tersebut dari lubang kecil .... (UN 2007)

Sebuah tabung berisi penuh zat cair (ideal). Pada dindingnya sejauh 20 cm dari permukaan atas terdapat lubang kecil (jauh lebih kecil dari penampang tabung) sehingga zat cair memancar (terlihat seperti pada gambar).

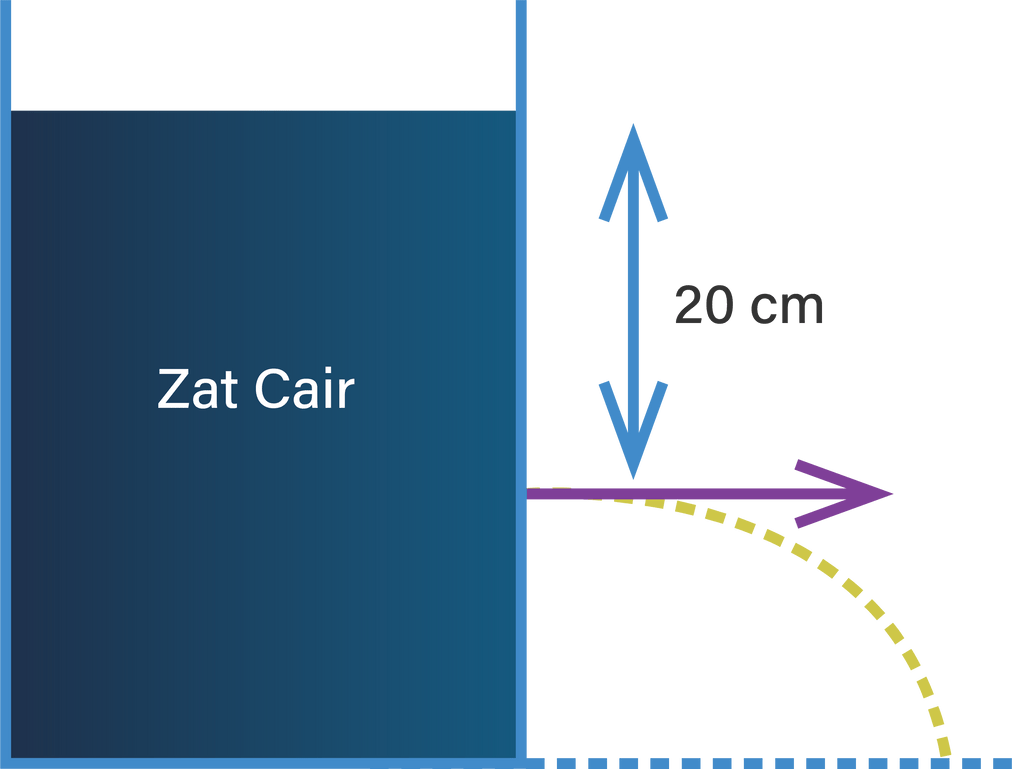
Besar kecepatan pancaran air tersebut dari lubang kecil .... $\;$

(UN 2007)

1,0 m/s $\;$
2,0 m/s $\;$
3,0 m/s $\;$
5,0 m/s $\;$
5,5 m/s $\;$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

J. Khairina

Master Teacher

Mahasiswa/Alumni Universitas Pendidikan Indonesia

Jawaban terverifikasi

Jawaban

jawaban yang tepat adalah B.

Pembahasan

Diketahui h = 20 cm = 0 , 2 m Ditanyakan Kecepatan pancaran air dari lubang kecil ( v ) Jawab Pada tangki yang berlubang, berlaku Teorema Torricelli yang merupakan turunan dari Hukum Bernoulli . Teorema Torricelli menyatakan bahwa " Kecepatan semburan air melalui lubang dengan jarak h dari permukaan air sama dengan kecepatan jatuh bebas air dari ketinggianh" . Kecepatan pancaran air dapat dihitung menggunakan rumus: v = 2 g h v = 2 ( 10 ) ( 0 , 2 ) v = 2 m / s Dengan demikian,besar kecepatan pancaran air tersebut dari lubang kecil adalah 2 m/s. Jadi, jawaban yang tepat adalah B.

Diketahui

$h = 20 cm = 0, 2 m$

Ditanyakan

Kecepatan pancaran air dari lubang kecil (v)

Jawab

Pada tangki yang berlubang, berlaku Teorema Torricelli yang merupakan turunan dari Hukum Bernoulli. Teorema Torricelli menyatakan bahwa "Kecepatan semburan air melalui lubang dengan jarak h dari permukaan air sama dengan kecepatan jatuh bebas air dari ketinggian h" .

Kecepatan pancaran air dapat dihitung menggunakan rumus:

$v = 2 g h v = 2 (10) (0, 2) v = 2 m / s$

Dengan demikian, besar kecepatan pancaran air tersebut dari lubang kecil adalah 2 m/s.

Jadi, jawaban yang tepat adalah B.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.8 (8 rating)

Pia Alfiyanti

Makasih ❤️

Pertanyaan serupa

Perhatikan gambar berikut! Air yang keluar dari lubang A akan jatuh sejauh x setelah menempuh waktu ....

5.0

Jawaban terverifikasi

Sebuah bak penampungan air setinggi 200 cm ( g = 10 m . s − 2 ) dan pada dinding terdapat lubang kebocoran (lihat gambar). Kelajuan air yang keluar dari lubang kebocoran tersebut adalah ...

5.0

Jawaban terverifikasi

Sebuah bak penampungan diisi air melalui keran seperti gambar di samping yang debitnya 1 liter per sekon. Jika luas lubang 5 cm 2 dan h 2 = 80 cm, hitung kecepatan air keluar dari lubang.

5.0

Jawaban terverifikasi

Sebuah tangki pada bagian dinding bawah terpasang kran seperti pada gambar. Tangki diisi penuh dengan air. Percepatan gravitasi = 10 m . s − 2 , maka saat kran dibuka kecepatan air mengalir dari kran ...

0.0

Jawaban terverifikasi

Air keluar dari suatu katup dibawah sebuah tangki pada kelajuan 6 m/s. Ketinggian air dalam tangki adalah ....

5.0

Jawaban terverifikasi