Pertanyaan

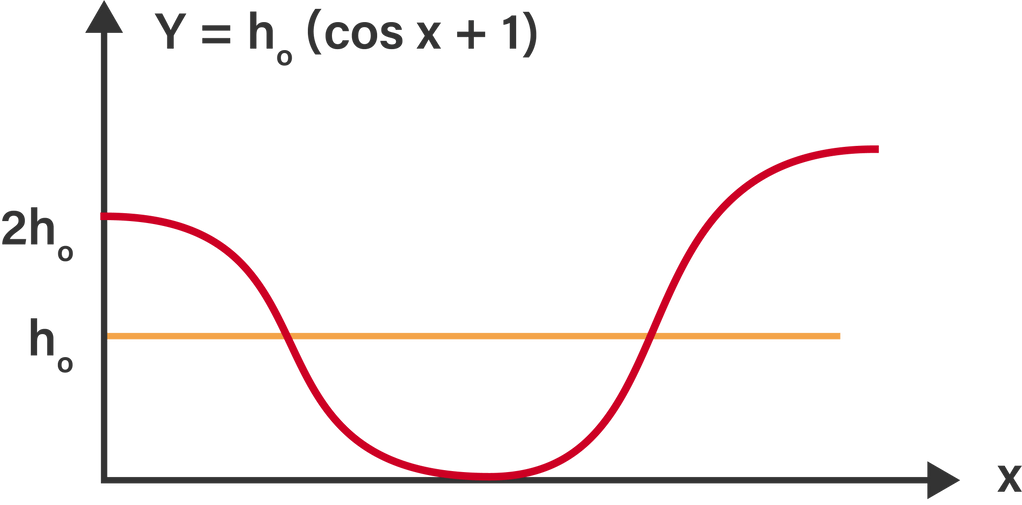
Sebuah bola kecil bermassa m meluncur di atas pemukaan licin dengan profiI mengikuti fungsi y = h o ( cos x + 1 ) , dengan y adalah ketinggian bola di atas sumbu horizontal x. Jika bola dilepas dari titik dengan ketinggian maksimum pada sumbu y, tanpa kecepatan awal, maka pernyataan yang tepat adalah .... kecepatan bola di titik terendah adalah 2 g h o kecepatan bola setengah dari kecepatan maksimun saat y = 4 7 h o energi mekanik bola adalah 2 m g h 0 energi kinetik bola sama dengan setengah darienergi mekanik saat kecepatannya 2 3 g h (SBMPTN 2016/SAINTEK/237129)

Sebuah bola kecil bermassa m meluncur di atas pemukaan licin dengan profiI mengikuti fungsi $y = h_{o} (cos x + 1)$ , dengan y adalah ketinggian bola di atas sumbu horizontal x. Jika bola dilepas dari titik dengan ketinggian maksimum pada sumbu y, tanpa kecepatan awal, maka pernyataan yang tepat adalah ....

kecepatan bola di titik terendah adalah $2 g h_{o}$
kecepatan bola setengah dari kecepatan maksimun saat $y = \frac{7}{4} h_{o}$
energi mekanik bola adalah $2 m g h_{0}$
energi kinetik bola sama dengan setengah dari energi mekanik saat kecepatannya $\frac{3 g h}{2}$

(SBMPTN 2016/SAINTEK/237129) $\;$

1, 2 dan 3 $\;$
1 dan 3 $\;$
2 dan 4 $\;$
hanya 4 $\;$
semua benar $\;$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

Y. Maghfirah

Master Teacher

Jawaban terverifikasi

Jawaban

Jawabannya adalah B.

Jawabannya adalah B. $\;$

Pembahasan

Diketahui bola kecil bermassa = m y = h o ( cos x + 1 ) v 0 = 0 m/s bola dilepas dari titik dengan ketinggian maksimum y maks Ditanyakan : pernyataan yang tepat adalah ... ? Penyelesaian : Perhatikan grafik fungsi di bawah ini, dimana fungsi gerak bola adalah y = h o ( cos x + 1 ) Ketinggian maksimumdicapai saat x = 0, sehingga y mak s = h o ( cos 0 ∘ + 1 ) = h o ( 1 + 1 ) = 2 h o Kecepatan bola di titik terendah dicapai saat S = y mak s = 2 h 0 v t 2 v t 2 v t 2 v t v t = = = = = v 0 2 + 2 g S 0 2 + 2 g ( 2 h 0 ) 4 g h 0 4 g h 0 2 g h 0 Kecepatan bola saat kecepatan setengah kecepatan maksimum dimana v mak s = 2 g h 0 v t = 2 1 v mak s = 2 1 2 g h 0 = g h 0 maka v t 2 g h 0 g h 0 S S = = = = = v 0 2 + 2 g S 0 2 + 2 g S 2 g S 2 g g h 0 2 h 0 sehingga y = y mak s − S = 2 h 0 − 2 h 0 = 2 3 h 0 Menentukan energi mekanik. Dititik tertinggi kita dapat menentukan energi mekanik. E m = = = Ep + E k m g ( 2 h 0 ) + o 2 m g h 0 Menentukan Kecepatan Menentukan kecepatan ketika Energi kinetik bola sama dengan setengah energi mekanik. E k = 2 1 E m = 2 1 2 m g h 0 = m g h 0 Sehingga E k m g h 0 v = = = 2 1 m v 2 2 1 m v 2 2 g h 0 Dari uraian di atas, maka pernyatan 1 dan 3 yang benar. Oleh karena itu, Jawabannya adalah B.

Diketahui

bola kecil bermassa = m

$y = h_{o} (cos x + 1)$

v₀ = 0 m/s

bola dilepas dari titik dengan ketinggian maksimum y_maks

Ditanyakan : pernyataan yang tepat adalah ... ?

Penyelesaian :

Perhatikan grafik fungsi di bawah ini, dimana fungsi gerak bola adalah $y = h_{o} (cos x + 1)$

Ketinggian maksimum dicapai saat x = 0, sehingga

$y_{mak s} = h_{o} (cos 0^{\circ} + 1) = h_{o} (1 + 1) = 2 h_{o}$

Kecepatan bola di titik terendah

dicapai saat $S = y_{mak s} = 2 h_{0}$
$v_{t}^{2} v_{t}^{2} v_{t}^{2} v_{t} v_{t} = = = = = v_{0}^{2} + 2 g S 0^{2} + 2 g (2 h_{0}) 4 g h_{0} 4 g h_{0} 2 g h_{0}$

Kecepatan bola saat kecepatan setengah kecepatan maksimum

dimana $v_{mak s} = 2 g h_{0}$

$v_{t} = \frac{1}{2} v_{mak s} = \frac{1}{2} 2 g h_{0} = g h_{0}$

maka

$v_{t}^{2} g h_{0} g h_{0} S S = = = = = v_{0}^{2} + 2 g S 0^{2} + 2 g S 2 g S \frac{g h _{0}}{2 g} \frac{h _{0}}{2}$

sehingga

$y = y_{mak s} - S = 2 h_{0} - \frac{h _{0}}{2} = \frac{3}{2} h_{0}$

Menentukan energi mekanik.

Dititik tertinggi kita dapat menentukan energi mekanik.

$E m = = = Ep + E k m g (2 h_{0}) + o 2 m g h_{0}$

Menentukan Kecepatan

Menentukan kecepatan ketika Energi kinetik bola sama dengan setengah energi mekanik.

$E k = \frac{1}{2} E m = \frac{1}{2} 2 m g h_{0} = m g h_{0}$

Sehingga

$E k m g h_{0} v = = = \frac{1}{2} m v^{2} \frac{1}{2} m v^{2} 2 g h_{0}$

Dari uraian di atas, maka pernyatan 1 dan 3 yang benar.

Oleh karena itu, Jawabannya adalah B. $\;$

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

0.0 (0 rating)

Pertanyaan serupa

Sebuah kotak bergerak dari keadaan diam menuruni suatu bidang miring yang panjang. Bagian pertama bidang miring itu licin dan bagian berikutnya sampai ke dasar bersifat kasar. Setelahbergerak selama b...

5.0

Jawaban terverifikasi

Sebuah bola bermassa M dilepaskan dari ketinggian h di atas permukaan tanah. Jika laju bola sesaat sebelum mencapai tanah adalah v , maka selama pergerakan bola .... Terjadi perubahan energi kin...

4.6

Jawaban terverifikasi

Sebuah beban bermassa m yang diikatkan pada ujung kanan sebuah pegas dengan konstanta pegas k diletakkan pada lantai datar dengan ujung pegas sebelah kiri terikat pada dinding. Beban ditarik ke kanan ...

0.0

Jawaban terverifikasi

Sebuah balok bemassa m dilepas dari keadaan diam pada puncak suatu bidang miring berkemiringan θ seperti diperlihatkan gambar berikut. Koefisien gesek statis dan kinetis antara balok dan bidang ...

0.0

Jawaban terverifikasi

Sebuah pot bunga terjatuh dari teras rumah di lantai satu yang jaraknya 5 meter dari permukaan tanah . Manakah pernyataan berikut yang benar terkait gerak jatuh pot bunga tersebut? ( EP = energi poten...

0.0

Jawaban terverifikasi