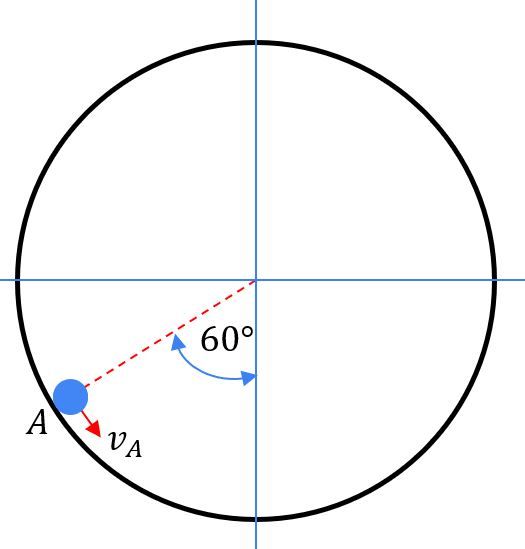
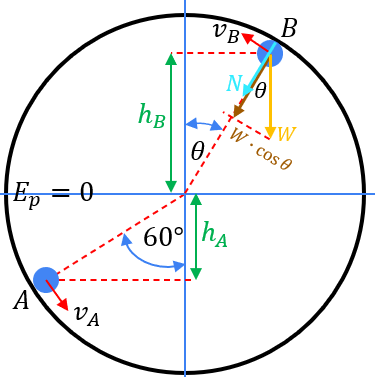
Sebuah benda m = 2 kg bergerak sepanjang sisi dalam sebuah lingkaran yang dipasang vertikal. DI titik A benda diberi kecepatan awal 5 m/s dengan jari-jari lintasannya 1 m, seperti pada gambar di bawah. Tentukan dimana dan dengan kecepatan berapa benda meninggalkan bidang lingkaran!

Pembahasan

Diketahui : Ditanya :dimana dan dengan kecepatan berapa benda meninggalkan bidang lingkaran? Penyelesaian : Asumsikan benda jatuh di B yang membentuk sudut dengan garis vertikal seperti yang ditunjukkan pada gambar. Benda akan lepas dari titik B jika gaya normal N yang bekerja pada bola sama dengan nol. Sehingga, dengan menggunakan Hukum Newton II untuk gaya sentripetal, kita dapatkan hubungan sebagai berikut: Selanjutnya, analisis hubungan antara benda di posisi A dan B dengan menggunakan hukum kekekalan energi mekanik, kita anggap garis horizontal yang melewati pusat lingkaran memiliki energi potensial nol, sehingga: Subtitusi persamaa (*) ke persamaan (**) Bola akan meninggalkan bidang lingkaran pada titik B yang memiliki sudut 60 o terhadap garis vertikal seperti yang ditunjukkan pada gambar. Selain itu, bisa dikatakakan bola meninggalkan bidang lingkaran setelah berputar 180 o . Kecepatan bola di titik B dapat dihitung dengan memasukkan sudut yang sudah didpatkan ke persamaan (*), yaitu: Jadi,Bola akan meninggalkan bidang lingkaran pada titik B yang memiliki sudut 60 o terhadap garis vertikal seperti yang ditunjukkan pada gambar. Kecepatan pada titik tersebut adalah